Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 45, 46 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Cho biết tỉ số \(e = \frac{c}{a}\) của các elip lần lượt là \(\frac{3}{4},\frac{1}{2},\frac{1}{4}\)(Hình 8). Tính tỉ số \(\frac{b}{a}\) theo \(e\) và nêu nhận xét về sự thay đổi của hình dạng elip gắn với hình chữ nhật cơ sở khi \(e\) thay đổi.
a) Tìm tâm sai của elip (E): \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{99}} = 1\) và elip (E’): \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{1} = 1\)
b) Không cần vẽ hình, theo bạn elip nào có hình dạng “dẹt” hơn?
Phương pháp giải:
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} - {b^2}} \)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
+ Khi tâm sai e càng lớn (tức là càng gần 1) thì elip trông càng “dẹt”.
Lời giải chi tiết:
a) Elip (E) có \({a^2} = 100,{b^2} = 99\), suy ra \(c = \sqrt {{a^2} - {b^2}} = 1,e = \frac{c}{a} = \frac{1}{{10}}.\)
Elip (E’) có \({a^2} = 10,{b^2} = 1\), suy ra \(c = \sqrt {{a^2} - {b^2}} = 3,e = \frac{c}{a} = \frac{3}{{\sqrt {10} }}.\)
b) Ta thấy \(\frac{3}{{\sqrt {10} }} > \frac{1}{{10}}\), vậy elip (E’) “dẹt” hơn elip (E).
Trong hệ Mặt Trời, các hành tinh chuyển động theo quỹ đạo là đường elip nhận tâm Mặt Trời là một tiêu điểm. Từ hình ảnh mô phỏng quỹ đạo chuyển động của các hành tinh (Hình 9), hãy so sánh tâm sai của quỹ đạo chuyển động của Trái Đất với tâm sai quỹ đạo chuyển động của tiểu hành tinh HD20782b.
(Nguồn: https://www.nasa.gov)
Phương pháp giải:
+ Khi tâm sai e càng lớn (tức là càng gần 1) thì elip trông càng “dẹt”.
Lời giải chi tiết:
Ta thấy quỹ đạo của tiểu hành tinh HD20782b dẹt hơn quỹ đạo của Trái Đất, suy ra tâm sai của elip quỹ đạo chuyển động của tiểu hành tinh lớn hơn tâm sai của elip quỹ đạo chuyển động của Trái Đất.
Cho biết tỉ số \(e = \frac{c}{a}\) của các elip lần lượt là \(\frac{3}{4},\frac{1}{2},\frac{1}{4}\)(Hình 8). Tính tỉ số \(\frac{b}{a}\) theo \(e\) và nêu nhận xét về sự thay đổi của hình dạng elip gắn với hình chữ nhật cơ sở khi \(e\) thay đổi.
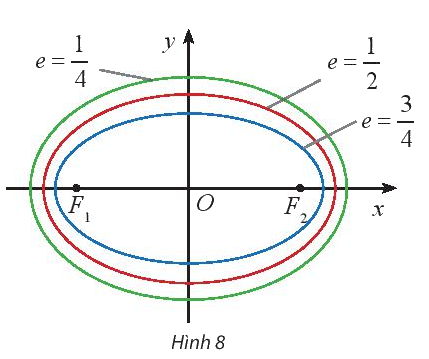
Lời giải chi tiết:
Ta có:
\(\frac{b}{a} = \frac{{\sqrt {{a^2} - {c^2}} }}{a} = \sqrt {1 - \frac{{{c^2}}}{{{a^2}}}} = \sqrt {1 - {e^2}} \)
Do đó:
- Khi tâm sai e càng bé (tức là càng gần 0) thì b càng gần a và elip trông càng “béo”.
- Khi tâm sai e càng lớn (tức là càng gần 1) thì tỉ số \(\frac{b}{a}\) càng gần 0 và elip trông càng “dẹt”.
Cho biết tỉ số \(e = \frac{c}{a}\) của các elip lần lượt là \(\frac{3}{4},\frac{1}{2},\frac{1}{4}\)(Hình 8). Tính tỉ số \(\frac{b}{a}\) theo \(e\) và nêu nhận xét về sự thay đổi của hình dạng elip gắn với hình chữ nhật cơ sở khi \(e\) thay đổi.
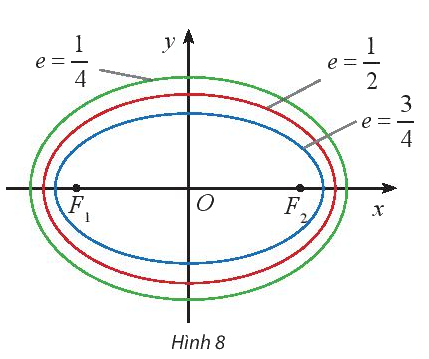
Lời giải chi tiết:
Ta có:
\(\frac{b}{a} = \frac{{\sqrt {{a^2} - {c^2}} }}{a} = \sqrt {1 - \frac{{{c^2}}}{{{a^2}}}} = \sqrt {1 - {e^2}} \)
Do đó:
- Khi tâm sai e càng bé (tức là càng gần 0) thì b càng gần a và elip trông càng “béo”.
- Khi tâm sai e càng lớn (tức là càng gần 1) thì tỉ số \(\frac{b}{a}\) càng gần 0 và elip trông càng “dẹt”.
a) Tìm tâm sai của elip (E): \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{99}} = 1\) và elip (E’): \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{1} = 1\)
b) Không cần vẽ hình, theo bạn elip nào có hình dạng “dẹt” hơn?
Phương pháp giải:
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} - {b^2}} \)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
+ Khi tâm sai e càng lớn (tức là càng gần 1) thì elip trông càng “dẹt”.
Lời giải chi tiết:
a) Elip (E) có \({a^2} = 100,{b^2} = 99\), suy ra \(c = \sqrt {{a^2} - {b^2}} = 1,e = \frac{c}{a} = \frac{1}{{10}}.\)
Elip (E’) có \({a^2} = 10,{b^2} = 1\), suy ra \(c = \sqrt {{a^2} - {b^2}} = 3,e = \frac{c}{a} = \frac{3}{{\sqrt {10} }}.\)
b) Ta thấy \(\frac{3}{{\sqrt {10} }} > \frac{1}{{10}}\), vậy elip (E’) “dẹt” hơn elip (E).
Trong hệ Mặt Trời, các hành tinh chuyển động theo quỹ đạo là đường elip nhận tâm Mặt Trời là một tiêu điểm. Từ hình ảnh mô phỏng quỹ đạo chuyển động của các hành tinh (Hình 9), hãy so sánh tâm sai của quỹ đạo chuyển động của Trái Đất với tâm sai quỹ đạo chuyển động của tiểu hành tinh HD20782b.
(Nguồn: https://www.nasa.gov)
Phương pháp giải:
+ Khi tâm sai e càng lớn (tức là càng gần 1) thì elip trông càng “dẹt”.
Lời giải chi tiết:
Ta thấy quỹ đạo của tiểu hành tinh HD20782b dẹt hơn quỹ đạo của Trái Đất, suy ra tâm sai của elip quỹ đạo chuyển động của tiểu hành tinh lớn hơn tâm sai của elip quỹ đạo chuyển động của Trái Đất.
Mục 3 của Chuyên đề học tập Toán 10 - Chân trời sáng tạo tập trung vào các kiến thức về vectơ trong mặt phẳng. Các bài tập trang 45 và 46 thường xoay quanh việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực), và ứng dụng các kiến thức này để giải quyết các bài toán hình học.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm cơ bản về vectơ:
Các bài tập trang 45 thường yêu cầu học sinh sử dụng tọa độ vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai vectơ cùng phương, hai đường thẳng song song, hoặc tìm tọa độ của một điểm thỏa mãn một điều kiện nào đó.
Ví dụ: Cho A(1, 2), B(3, 4), C(5, 2). Chứng minh rằng A, B, C thẳng hàng.
Lời giải:
Các bài tập trang 46 thường tập trung vào việc thực hiện các phép toán vectơ và ứng dụng chúng để giải quyết các bài toán cụ thể.
Ví dụ: Cho vectơ a = (1, -2) và vectơ b = (3, 1). Tính vectơ 2a - b.
Lời giải:
2a = 2(1, -2) = (2, -4)
2a - b = (2, -4) - (3, 1) = (2-3, -4-1) = (-1, -5)
Để củng cố kiến thức và kỹ năng giải bài tập vectơ, các em nên luyện tập thêm với các bài tập khác trong sách giáo khoa và các tài liệu tham khảo. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp các em tự tin hơn trong quá trình học tập.
Hy vọng với những hướng dẫn chi tiết này, các em sẽ giải quyết thành công các bài tập mục 3 trang 45, 46 Chuyên đề học tập Toán 10 - Chân trời sáng tạo. Chúc các em học tốt!