Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và phù hợp với chương trình học Toán 10 hiện hành. Hãy cùng theo dõi để nắm vững kiến thức nhé!
Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bang sau.
Đề bài
Một cửa hàng giải khát chỉ phục vụ ba loại sinh tố: xoài, bơ và mãng cầu. Để pha mỗi li (cốc) sinh tố này đều cần dùng đến sữa đặc, sữa tươi và sữa chua với công thức cho ở bang sau.
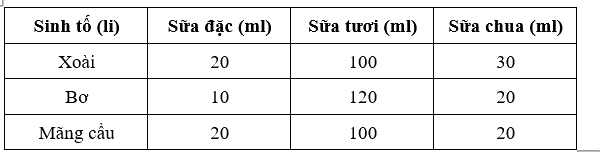
Ngày hôm qua cửa hàng đã dùng hết 2 l sữa đặc, 12,8 l sữa tươi và 2,9 l sữa chua. Cửa hàng đã bán được bao nhiêu li sinh tố mỗi loại trong ngày hôm qua?
Lời giải chi tiết
Gọi số li sinh tố xoài, bơ mãng cầu mà cửa hàng đã bán trong ngày hôm qua lần lượt là x, y, z (li).
\(\left( {x,y,z \in \mathbb{N}} \right)\)
Đổi 2 l = 2000 ml; 12,8 l = 12800 ml và 2,9 l = 2900 ml.
Ngày hôm qua cửa hàng đã dùng hết 2 l sữa đặc, 12,8 l sữa tươi và 2,9 l sữa chua nên ta có:
\(\left\{ \begin{array}{l}20x + 10y + 20z = 2000\\100x + 120y + 100z = 12800\\30x + 20y + 20z = 2900\end{array} \right.\)
Dùng máy tính cầm tay, giải hpt ta được \(x = 50,y = 40,z = 30\)
Vậy ngày hôm qua cửa hàng đã bán 50 li sinh tố xoài, 40 li sinh tố bơ và 30 li sinh tố mãng cầu.
Bài 3 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh chứng minh đẳng thức vectơ, tìm tọa độ điểm, hoặc xác định mối quan hệ giữa các điểm dựa trên vectơ.
Để giải quyết bài 3 trang 21 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 3 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo:
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.
Lời giải:
Đề bài: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng overrightarrow{OA} +overrightarrow{OB} +overrightarrow{OC} +overrightarrow{OD} =overrightarrow{0}.
Lời giải:
Để củng cố kiến thức về vectơ và ứng dụng trong hình học, học sinh có thể tự giải các bài tập tương tự sau:
Khi giải bài tập về vectơ, học sinh cần chú ý:
Bài 3 trang 21 Chuyên đề học tập Toán 10 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ trong hình học. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.