Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này được giaitoan.edu.vn biên soạn với mục đích giúp các em hiểu rõ hơn về kiến thức và phương pháp giải bài tập trong chuyên đề.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các lưu ý quan trọng để các em có thể tự tin giải quyết các bài toán tương tự.
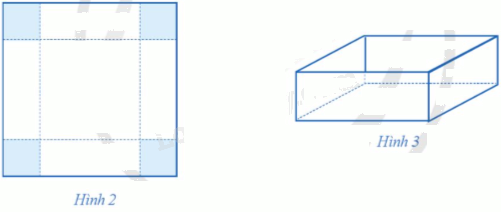
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng (x) (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương (x) để làm được cái hộp đựng đồ có thể tích lớn nhất.
Đề bài
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương \(x\) để làm được cái hộp đựng đồ có thể tích lớn nhất.
Phương pháp giải - Xem chi tiết
Thiết lập hàm số tính thể tích hộp và tìm giá trị lớn nhất của hàm số đó.
Lời giải chi tiết
Cạnh đáy hình vuông của chiếc hộp không nắp là \(60 - 2x\) (cm).
Khi đó ta có \(60 - 2x \le 37\) hay \(x \ge 11,5.\)
Chiều cao của chiếc hộp không nắp là \(x\) (cm). Khi đó ta có \(x \le 28.\)
Diện tích đáy của chiếc hộp không nắp là \({(60 - 2x)^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Thể tích của chiếc hộp không nắp là \(x{(60 - 2x)^2} = x(3600 - 240x + 4{x^2}) = 3600x - 240{x^2} + 4{x^3}\) (\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
Xét hàm số \(f(x) = 3600x - 240{x^2} + 4{x^3}\) với \(11,5 \le x \le 28.\)
Ta có \(f'(x) = 3600 - 480x + 12{x^2}.\)
Xét \(f'(x) = 0 \Leftrightarrow 3600 - 480x + 12{x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10(ktm)\\x = 30(ktm)\end{array} \right.\)
Ta có bảng biến thiên:
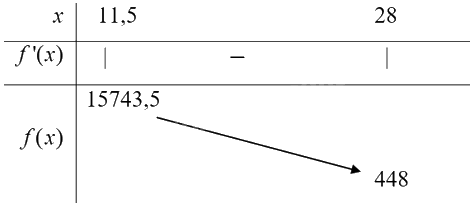
Căn cứ vào yêu cầu bài toán ta có \(\mathop {\max }\limits_{(0; + \infty )} f(x) = f(11,5) = 15743,5\) tại \(x = 11,5.\)
Vậy \(x = 11,5\) thì cái hộp có thể tích lớn nhất.
Bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm, định lý và công thức liên quan. Bài viết này sẽ cung cấp một hướng dẫn chi tiết, từng bước để giải bài tập, đồng thời giải thích rõ ràng các bước thực hiện.
Trước khi bắt đầu giải bài, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này bao gồm việc xác định các thông tin đã cho, các thông tin cần tìm và các điều kiện ràng buộc. Trong bài 1 trang 35, học sinh cần chú ý đến các yếu tố sau:
Dưới đây là lời giải chi tiết cho bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu:
Để giải bài toán này, chúng ta cần áp dụng kiến thức về [Điền kiến thức liên quan]. Cụ thể, chúng ta sẽ sử dụng công thức [Điền công thức liên quan] để tính toán.
Sau khi đã xác định được công thức cần sử dụng, chúng ta sẽ tiến hành thực hiện các phép tính để tìm ra kết quả. Lưu ý rằng cần phải thực hiện các phép tính một cách cẩn thận và chính xác.
Sau khi đã tìm được kết quả, chúng ta cần kiểm tra lại để đảm bảo rằng kết quả đó là chính xác và phù hợp với yêu cầu của bài toán. Chúng ta có thể kiểm tra kết quả bằng cách thay thế lại vào đề bài hoặc sử dụng các phương pháp kiểm tra khác.
Để giúp các em hiểu rõ hơn về cách giải bài 1 trang 35, chúng ta sẽ xem xét một ví dụ minh họa cụ thể:
Ví dụ: [Nêu một ví dụ cụ thể liên quan đến bài 1 trang 35].
Giải: [Giải ví dụ một cách chi tiết và dễ hiểu].
Khi giải bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều, các em cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể thử giải các bài tập tương tự sau:
Bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em sẽ có thể tự tin giải quyết bài toán một cách hiệu quả. Chúc các em học tập tốt!
| Khái niệm | Định nghĩa |
|---|---|
| [Khái niệm 1] | [Định nghĩa 1] |
| [Khái niệm 2] | [Định nghĩa 2] |