Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh diều. Chúng tôi hiểu rằng việc giải các bài tập Toán 12 có thể gặp nhiều khó khăn, đặc biệt là với các chuyên đề mới.
Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải, các kiến thức liên quan và đáp án chính xác cho hoạt động mở đầu này.
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau: Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít. Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít. Công ty có 120 lít nước anh đào và 150 lít nước cam. Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Trả lời câu hỏi Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 Cánh diều
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau:
Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít.
Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít.
Công ty có 120 lít nước anh đào và 150 lít nước cam.
Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Phương pháp giải:
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{{a}_{1}}x+{{b}_{1}}y\le {{c}_{1}} \\{{a}_{2}}x+{{b}_{2}}y\le {{c}_{2}}\\...\\{{a}_{k}}x+{{b}_{k}}y\le {{c}_{k}}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết:
Gọi \(x,y\) lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất (\(x \ge 0;y \ge 0\))
Tổng số tiền công ty thu được khi bán \(x\) lít nước sinh tố loại thứ nhất và \(y\) lít nước sinh tố loại tứ hai là \(T = 24x + 18y\) (nghìn đồng).
Số lít nước anh đào có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,7x + 0,4y\) (lít)
Số lít nước anh cam có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,3x + 0,6y\) (lít)
Vì công ty có 120 lít nước anh đào và 150 lít nước cam nên lượng nguyên liệu sử dụng không vượt qua mức dự trữ trên do đó ta có hệ bất phương trình \(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\end{array} \right.\)
Để tổng số tiền công ty thu được là nhiều nhất thì ta có bài toán quy hoạch tuyến tính sau: \(\left\{ \begin{array}{l}\max (T = 24x + 18y)\\0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:
\(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\)(II) | 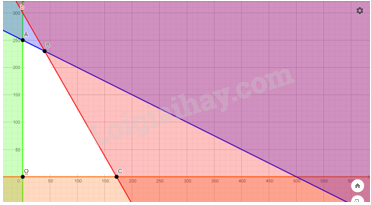 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 24x + 18y\) khi \((x,y)\) là nghiệm của hệ bất phương trình (II).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với \(O(0;0);\) \(A(0;250);\) \(B(40;230)\); \(C\left( {\frac{{1200}}{7};0} \right)\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 24x + 18y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;250) = 4500;\) \(T(40;230) = 5100;\) \(T\left( {\frac{{1200}}{7};0} \right) = \frac{{28800}}{7}.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(40;230) = 5100\)
Bước 4. Vì 40 và 230 đều thỏa mãn yêu cầu bài toán nên nên cặp số \((40;230)\) là nghiệm của bài toán (I).
Vậy để số công ty thu được nhiều tiền nhất thì cần sản xuất 40 lít nước loại thứ nhất và 230 lít nước loại thứ hai.
Trả lời câu hỏi Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 Cánh diều
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau:
Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít.
Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít.
Công ty có 120 lít nước anh đào và 150 lít nước cam.
Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Phương pháp giải:
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{{a}_{1}}x+{{b}_{1}}y\le {{c}_{1}} \\{{a}_{2}}x+{{b}_{2}}y\le {{c}_{2}}\\...\\{{a}_{k}}x+{{b}_{k}}y\le {{c}_{k}}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết:
Gọi \(x,y\) lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất (\(x \ge 0;y \ge 0\))
Tổng số tiền công ty thu được khi bán \(x\) lít nước sinh tố loại thứ nhất và \(y\) lít nước sinh tố loại tứ hai là \(T = 24x + 18y\) (nghìn đồng).
Số lít nước anh đào có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,7x + 0,4y\) (lít)
Số lít nước anh cam có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,3x + 0,6y\) (lít)
Vì công ty có 120 lít nước anh đào và 150 lít nước cam nên lượng nguyên liệu sử dụng không vượt qua mức dự trữ trên do đó ta có hệ bất phương trình \(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\end{array} \right.\)
Để tổng số tiền công ty thu được là nhiều nhất thì ta có bài toán quy hoạch tuyến tính sau: \(\left\{ \begin{array}{l}\max (T = 24x + 18y)\\0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:
\(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\)(II) | 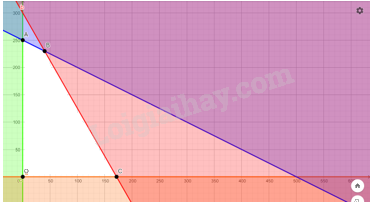 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 24x + 18y\) khi \((x,y)\) là nghiệm của hệ bất phương trình (II).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với \(O(0;0);\) \(A(0;250);\) \(B(40;230)\); \(C\left( {\frac{{1200}}{7};0} \right)\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 24x + 18y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;250) = 4500;\) \(T(40;230) = 5100;\) \(T\left( {\frac{{1200}}{7};0} \right) = \frac{{28800}}{7}.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(40;230) = 5100\)
Bước 4. Vì 40 và 230 đều thỏa mãn yêu cầu bài toán nên nên cặp số \((40;230)\) là nghiệm của bài toán (I).
Vậy để số công ty thu được nhiều tiền nhất thì cần sản xuất 40 lít nước loại thứ nhất và 230 lít nước loại thứ hai.
Hoạt động mở đầu trang 20 trong Chuyên đề học tập Toán 12 - Cánh diều thường đóng vai trò quan trọng trong việc giới thiệu một khái niệm mới hoặc một phương pháp tiếp cận mới trong toán học. Nó thường được thiết kế để kích thích tư duy của học sinh, khuyến khích họ tự khám phá và xây dựng kiến thức. Việc giải quyết thành công hoạt động này là nền tảng để học sinh tiếp thu các kiến thức tiếp theo trong chuyên đề.
Để giải quyết hiệu quả Hoạt động mở đầu trang 20, trước tiên cần phải đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, hoạt động này sẽ yêu cầu học sinh thực hiện một hoặc nhiều nhiệm vụ sau:
Dưới đây là một số phương pháp giải Hoạt động mở đầu trang 20 mà bạn có thể áp dụng:
Giả sử Hoạt động mở đầu trang 20 yêu cầu học sinh phân tích một tình huống thực tế về việc tính toán lãi suất ngân hàng. Để giải quyết hoạt động này, học sinh cần:
Khi giải Hoạt động mở đầu trang 20, bạn cần lưu ý những điều sau:
Giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh diều là một cơ hội tuyệt vời để bạn rèn luyện tư duy, kỹ năng giải quyết vấn đề và áp dụng kiến thức vào thực tế. Hãy tận dụng cơ hội này để học tập và phát triển bản thân.