Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học toán một cách dễ dàng và thú vị.
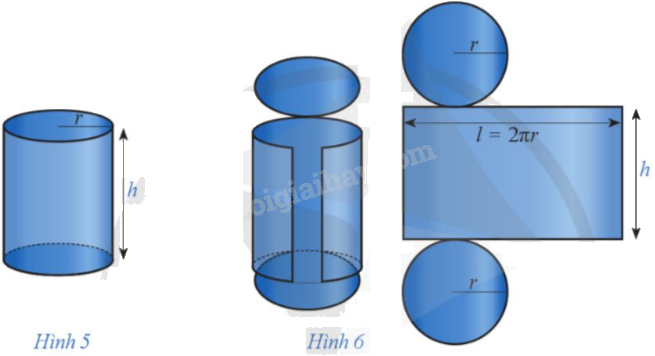
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
Đề bài
Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
Phương pháp giải - Xem chi tiết
+) Từ thể tích của hộp đựng nước giải khát ta sẽ biểu diễn được chiều cao của hộp nước theo bán kính đáy của nó \(h = \frac{{500}}{{\pi {r^2}}}\)
+) Diện tích vỏ hộp chính là diện tích toàn phần của hộp nước hình trụ.
+) Ta sẽ biểu diễn được diện tích vỏ hộp bằng một hàm số \(S(r)\)ẩn r
+) Yêu cầu bài toán đồng nghĩa với việc ta phải đi tìm bán kính, chiều cao mà ở đó hàm số \(S(r)\)đạt giá trị nhỏ nhất.
Lời giải chi tiết
Chiều cao \(h\) của hộp đứng nước có dạng hình trụ là \(h = \frac{{500}}{{\pi {r^2}}}\) (cm).
Diện tích mặt đáy của hộp đựng nước là \({S_{\rm{d}}} = \pi {r^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Diện tích xung quanh của hộp đựng nước là \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{500}}{{\pi {r^2}}} = \frac{{1000}}{r}{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\)
Diện tích vỏ hộp là \(S = 2\pi {r^2} + \frac{{1000}}{r}({\rm{c}}{{\rm{m}}^{\rm{2}}})\).
Xét hàm số \(S(r) = 2\pi {r^2} + \frac{{1000}}{r},r \in (0; + \infty ).\)
Ta có \(S'(r) = 4\pi r - \frac{{1000}}{{{r^2}}}.\) Do đó \(S'(r) = 0 \Leftrightarrow r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}.\)
Ta có bảng biến thiên của hàm số \(S(r)\) như sau:
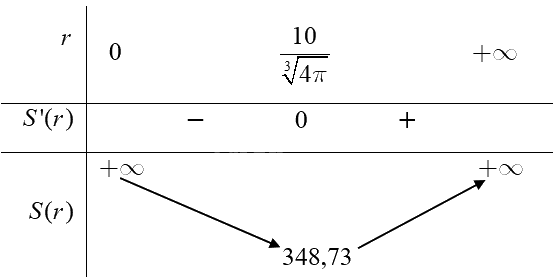
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(r) \approx 348,73\) tại \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm).
Vậy để diện tích vỏ hộp là nhỏ nhất thì bán kính của chiếc hộp là \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm) và chiều cao của chiếc hộp là \(h = \frac{{500}}{{\pi {{\left( {\frac{{10}}{{\sqrt[3]{{4\pi }}}}} \right)}^2}}} = \frac{{5{{\left( {\sqrt[3]{{4\pi }}} \right)}^2}}}{\pi }\) (cm).
Bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề quan trọng như đạo hàm, tích phân, số phức và hình học không gian. Việc giải bài tập trong chuyên đề này không chỉ giúp học sinh hiểu sâu hơn về lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Bài 8 trang 37 bao gồm một loạt các bài tập khác nhau, từ các bài tập cơ bản đến các bài tập nâng cao, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Các bài tập thường xoay quanh các chủ đề sau:
Để giải bài tập bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều một cách hiệu quả, học sinh cần:
Bài tập: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5.
Để học tốt Toán 12, các em nên:
Bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải quyết vấn đề. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.
| Chủ đề | Mức độ khó |
|---|---|
| Đạo hàm | Trung bình |
| Tích phân | Khó |
| Số phức | Trung bình |
| Hình học không gian | Khó |