Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
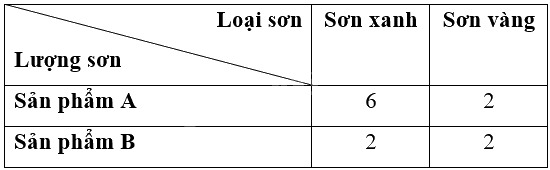
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm). Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.
Đề bài
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm).
Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.
Phương pháp giải - Xem chi tiết
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết
Gọi \(x,y\) lần lượt là số sản phẩm loại A và loại B người đó cần sơn \((x \in N;y \in N)\)
Số tiền lãi người đó thu được là \(T = 10x + 8y\) (triệu đồng)
Vì người đó sử dụng không quá 12 kg sơn xanh nên ta có \(6x + 2y \le 12;\)
Vì người đó sử dụng không quá 8 kg sơn vàng nên ta có \(2x + 2y \le 8;\)
Do người đó muốn số tiền lãi thu được là lớn nhất nên ta có bài toán quy hoạch tuyến tính \(\left\{ \begin{array}{l}\max (T = 10x + 8y)\\6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là số thực) sau:
\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (II)
 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 10x + 8y\) khi \((x,y)\) thoả mãn bất phương trình (II)
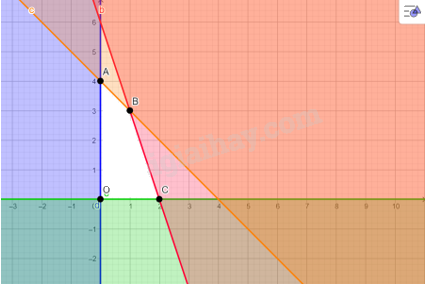
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);\) \(A(0;4);\) \(B(1;3)\); \(C(2;0).\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 10x + 8y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;4) = 32;\) \(T(1;3) = 34;\) \(T(2;0) = 20.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(1;3) = 34.\)
Bước 4. Vì 1 và 3 đều là các số tự nhiên nên cặp số \((1;3)\) là nghiệm của bài toán (I).
Vậy để số tiền lãi thu được là lớn nhất thì cần sơn 1 sản phẩm loại A và 3 sản phẩm loại B.
Bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là vô cùng quan trọng để giải quyết bài toán này một cách hiệu quả.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước, hoặc tìm điều kiện để hàm số có cực trị. Việc hiểu rõ yêu cầu của đề bài sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
Để giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều, chúng ta có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên khoảng [0, 3].
Vậy, giá trị lớn nhất của hàm số trên khoảng [0, 3] là 2, đạt được tại x = 0 và x = 3. Giá trị nhỏ nhất của hàm số trên khoảng [0, 3] là -2, đạt được tại x = 2.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn trong các kỳ thi.
Bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập một cách hiệu quả. Chúc bạn học tốt!