Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 36 Chuyên đề học tập Toán 12 - Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài tập và lời giải cho các môn Toán từ cấp THCS đến THPT.
Một nhà máy sản xuất xe đạp cho thị trường châu Âu theo đơn giá 120 euro (€). Chi phí mỗi ngày của nhà máy được cho bởi hàm số (K(x) = 0,02{x^3} - 3{x^2} + 172x + 2400.) trong đó (x) là số lượng xe đạp sản xuất được trong ngày hôm đó. Mỗi ngày có thể sản xuất tối đa 130 xe đạp. Giả sử số xe đạp sản xuất được trong mỗi ngày đề được bán hết vào cuối ngày đó. Gọi (G(x)) là hàm biểu diễn lợi nhuận hằng ngày của nhà máy. a) Vẽ đồ thị hàm số (G(x)) trên đoạn (left[ {0;130} right].) b
Đề bài
Một nhà máy sản xuất xe đạp cho thị trường châu Âu theo đơn giá 120 euro (€). Chi phí mỗi ngày của nhà máy được cho bởi hàm số
\(K(x) = 0,02{x^3} - 3{x^2} + 172x + 2400.\)
trong đó \(x\) là số lượng xe đạp sản xuất được trong ngày hôm đó. Mỗi ngày có thể sản xuất tối đa 130 xe đạp. Giả sử số xe đạp sản xuất được trong mỗi ngày đề được bán hết vào cuối ngày đó.
Gọi \(G(x)\) là hàm biểu diễn lợi nhuận hằng ngày của nhà máy.
a) Vẽ đồ thị hàm số \(G(x)\) trên đoạn \(\left[ {0;130} \right].\)
b) Số lượng xe mỗi ngày cần sản xuất là bao nhiêu để nhà máy có lãi?
c) Số lượng xe mỗi ngày cần sản xuất là bao nhiêu để nhà máy có lợi nhuận lớn nhất?
d) Giả sử nhà máy quyết định tận dụng tối đa công suất sản xuất 130 xe đạp mỗi ngày. Nhà máy phải chọn đơn giá là bao nhiêu để có lãi?
Phương pháp giải - Xem chi tiết
+) Biểu diễn doanh thu một ngày của nhà máy \(P(x) = 120x\) (€), \(x \in {\rm{[0;130]}}\).
+) Lợi nhuận hằng ngày của nhà máy chính bằng hiệu của doanh thu và chi phí sản xuất trong một ngày tức \(G(x) = P(x) - K(x)\)
+) Để vẽ đồ thị hàm số \(G(x)\) ta cần xét tính đơn điệu của hàm số này, xác định các điểm của đồ thị hàm số cắt trục tung và trục hoành
+) Để sản xuất có lãi tức là lợi nhuận thu được phải dương hay \(G(x) > 0\)
+) Để lợi nhuận lớn nhất tức \(G(x)\)đạt giá trị lớn nhất. Ta cần tìm \(x\) để \(G(x)\)đạt giá trị lớn nhất (dựa vào bảng biến thiên) cần lưu ý \(x\) là số tự nhiên.
+) Gọi y là đơn giá mới, ta cần biểu diễn doanh thu theo y. Từ đó ta được một hàm doanh thu mới, ta cần tìm giá trị lớn nhất của hàm số này.
Lời giải chi tiết
a) Doanh thu một ngày của nhà máy sản xuất là \(P(x) = 120x\) (€), \(x \in {\rm{[0;130]}}\).
Lợi nhuận một ngày của nhà máy là
\(G(x) = P(x) - K(x) = 120x - (0,02{x^3} - 3{x^2} + 172x + 2400)\)
\(G(x) = - 0,02{x^3} + 3{x^2} - 52x - 2400\) (€),
Vẽ đồ thị hàm số \(G(x)\) trên đoạn \({\rm{[}}0;130]\):

\(G'(x) = 0 \Leftrightarrow x \approx 9,6\) hoặc \(x \approx 90,4.\)
Bảng biến thiên:
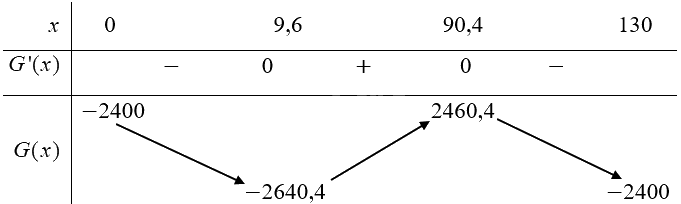
Hàm số nghịch biến trên \({\rm{[}}0;9,6)\) và \((90,4;130]\); đồng biến trên khoảng \((9,6;90,4)\).
a) Để nhà máy có lãi thì \(G(x) > 0\).
Từ đồ thị hàm số ở câu a, ta có \(G(x) > 0 \Leftrightarrow x \in (50;120)\).
Mà số lượng xe là số tự nhiên nên \(x \in N\) do đó \(x \in {\rm{[}}51;119]\)
Vậy mỗi ngày phải sản xuất từ 51 dến 119 chiếc xe để có lãi.
b) Từ bảng biến thiên của hàm số \(G(x)\) ở câu a, ta có \(G(x)\) đạt giá trị lớn nhất khi và chỉ khi \(x \approx 90,4\). Vì \(x\) là số tự nhiên nên \(x = 90\) hoặc \(x = 91\) thì lợi nhuận sẽ thu được lớn nhất.
Ta có \(G(90) = 2640\) và \(G(91) = 2639,58\) nên \(G(90) > G(91)\).
Vậy để nhà máy có lợi nhất thì mỗi ngày xần sản xuất 90 chiếc xe máy.
c) Chi phí mỗi ngày của nhà máy khi sản xuất 130 chiếc xe là:
\(K(130) = {0,02.130^3} - {3.130^2} + 172.130 + 2400 = 18000\) (€).
Gọi \(y\)(€) là đơn giá nhà máy bán ra thị trường, khi đó doanh thu nhà máy thu được là \(P(y) = 130y\) (€).
Lợi nhuận nhà máy thu được là \(G(y) = P(y) - K(130) = 130y - 18000\) (€).
Để nhà máy có lãi thì \(G(y) > 0 \Leftrightarrow 130y - 18000 > 0 \Leftrightarrow y > \frac{{1800}}{{13}} \approx 138,46\).
Vậy để nhà máy có lãi thì cần chọn đơn giá lớn hơn 138,46 euro.
Bài 5 trang 36 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề quan trọng như đạo hàm, tích phân, số phức và hình học không gian. Việc nắm vững kiến thức này là nền tảng để các em học sinh có thể giải quyết các bài toán phức tạp hơn trong kỳ thi THPT Quốc gia.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 36, chúng ta sẽ đi vào giải chi tiết từng câu hỏi. Dưới đây là lời giải chi tiết cho một số câu hỏi tiêu biểu:
Lời giải:
f'(x) = 3x2 - 4x + 5
Lời giải:
g'(x) = 4x3 - 8x
Giải phương trình g'(x) = 0, ta được x = 0, x = √2, x = -√2
Lập bảng biến thiên, ta thấy hàm số đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.
Lời giải:
Lấy logarit cơ số 2 hai vế, ta được x = log25
Để giải bài tập Toán 12 hiệu quả, các em học sinh cần:
Ngoài sách giáo khoa và sách bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải bài 5 trang 36 Chuyên đề học tập Toán 12 - Cánh diều và đạt kết quả tốt trong kỳ thi THPT Quốc gia. Chúc các em học tập tốt!