Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
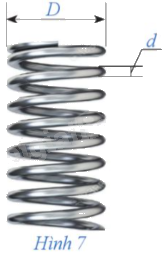
Một lò xo được làm từ một sợi dây kim loại. Gọi (d) là đường kính (trung bình) của sợ dây kim loại và (D) là đường kính (trung bình) của lò xo (Hình 7). Ki lò xo đứng lên mặt đất thì nó nén lại bởi trọng lượng (P) của lò xo, vật chất trong dây kim loại chịu ứng suất lớn nhất (S) tại các điểm trên bè mặt sợi dây mà khoảng cách từ những điểm đó đến đường tâm của lò so là nhỏ nhất. Biết rằng (S) được cho bởi công thức: (S = frac{{8PD}}{{pi {d^3}}}left[ {frac{{frac{{4D}}{d} - 1}}{{
Đề bài
Một lò xo được làm từ một sợi dây kim loại. Gọi \(d\) là đường kính (trung bình) của sợ dây kim loại và \(D\) là đường kính (trung bình) của lò xo (Hình 7). Ki lò xo đứng lên mặt đất thì nó nén lại bởi trọng lượng \(P\) của lò xo, vật chất trong dây kim loại chịu ứng suất lớn nhất \(S\) tại các điểm trên bè mặt sợi dây mà khoảng cách từ những điểm đó đến đường tâm của lò so là nhỏ nhất.
Biết rằng \(S\) được cho bởi công thức:
\(S = \frac{{8PD}}{{\pi {d^3}}}\left[ {\frac{{\frac{{4D}}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right].\)
 |
a) Giả sử sợi dây kim loại là cố định. Hỏi ta phải cuộn sợi dây kim loại đó thành lò xo với đường kình \(D\) bằng bao nhiêu để ứng xuất \(S\) là nhỏ nhất?
b) Giả sử lò xo có đường kính \(D\) cố định. Hỏi ta phải chọn loại dây kim loại với đường kính \(d\) bằng bao nhiêu để ứng suất \(S\) là nhỏ nhất.
Phương pháp giải - Xem chi tiết
a) Khi sợi dây kim loại cố định thì \(d\) và \(P\) là các hằng số.
Khi đó, để dễ dàng trong tính toán ta đặt \(a = \frac{D}{d}(a > 0).\)
Biểu diễn lại \(S\) ta có: \(S(a) = \frac{{8Pa}}{{\pi {d^2}}}\left[ {\frac{{4a - 1}}{{4(a - 1)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{4{a^2} - a}}{{4(a - 1)}} + 0,615} \right]\)
Ta sẽ đi tìm giá trị nhỏ nhất của hàm số \(S(a)\).
b) Làm tương tự với câu a.
Lời giải chi tiết
a) Khi sợi dây kim loại cố định thì \(d\) và \(P\) là các hằng số.
Đặt \(a = \frac{D}{d}(a > 0).\)
Khi đó ta có hàm số \(S(a) = \frac{{8Pa}}{{\pi {d^2}}}\left[ {\frac{{4a - 1}}{{4(a - 1)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{4{a^2} - a}}{{4(a - 1)}} + 0,615} \right]\) với \(a > 0.\)
Ta có: \(S'(a) = \frac{{8P}}{{\pi {d^2}}}\left[ {\frac{{(8a - 1).4(a - 1) - (4{a^2} - a).4}}{{16{{(a - 1)}^2}}}} \right] = \frac{{2P}}{{\pi {d^2}}}.\frac{{4{a^2} - 8a + 1}}{{{{(a - 1)}^2}}}.\)
Do đó \(S'(a) = 0 \Leftrightarrow 4{a^2} - 8a + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{2 - \sqrt 3 }}{2}\\a = \frac{{2 + \sqrt 3 }}{2}\end{array} \right.\)
Ta có bảng biến thiên:
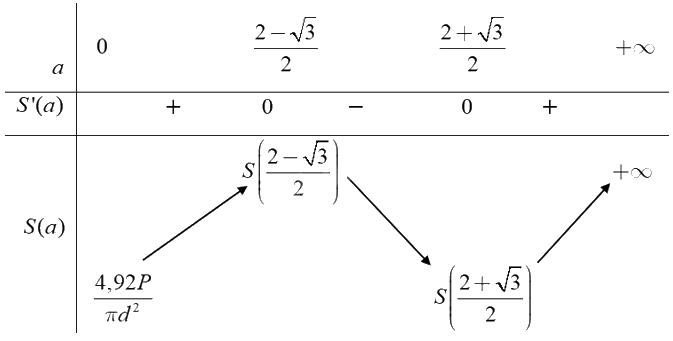
Căn cứ vào bảng biến thiên, ta có \(\mathop {\min }\limits_{(0; + \infty )} S(a) = S\left( {\frac{{2 + \sqrt 3 }}{2}} \right)\) tại \(a = \frac{{2 + \sqrt 3 }}{2}\) hay \(\frac{D}{d} = \frac{{2 + \sqrt 3 }}{2}\) suy ra \(D = \frac{{2 + \sqrt 3 }}{2}d.\)
b) Với \(d > 0\) ta có:
\(S(d) = \frac{{8PD}}{{\pi {D^2}}}\left[ {\frac{{4\frac{D}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right] = \frac{{8P}}{{\pi {D^2}}}.{\left( {\frac{D}{d}} \right)^3}.\left[ {\frac{{4\frac{D}{d} - 1}}{{4\left( {\frac{D}{d} - 1} \right)}} + \frac{{0,615d}}{D}} \right]\)
Đặt \(a = \frac{D}{d}(a > 0).\)
Khi đó ta có hàm số \(S(a) = \frac{{8P{a^3}}}{{\pi {D^2}}}.\left[ {\frac{{4a - 1}}{{4\left( {a - 1} \right)}} + \frac{{0,615}}{a}} \right] = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{4{a^4} - {a^3}}}{{4\left( {a - 1} \right)}} + 0,615{a^2}} \right]\)
Ta có \(S'(a) = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{(16{a^3} - 3{a^2}).4(a - 1) - (4{a^4} - {a^3}).4}}{{16{{\left( {a - 1} \right)}^2}}} + 1,23a} \right]\)
\(S'(a) = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{12{a^4} - 18{a^3} + 3{a^2}}}{{4{{\left( {a - 1} \right)}^2}}} + 1,23a} \right] = \frac{{8P}}{{\pi {D^2}}}.\left[ {\frac{{12{a^4} - 18{a^3} + 3{a^2} + 1,23a.4{{\left( {a - 1} \right)}^2}}}{{4{{\left( {a - 1} \right)}^2}}}} \right]\)
\(S'(a) = \frac{{2P}}{{\pi {D^2}}}.\frac{{12{a^4} - 13,08{a^3} - 6,84{a^2} + 4,92a}}{{{{\left( {a - 1} \right)}^2}}}.\)
Do đó \(S'(a) = 0 \Leftrightarrow 12{a^4} - 13,08{a^3} - 6,84{a^2} + 4,92a = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0(ktm)\\x \approx 1,285\\x \approx 0,476\end{array} \right.\)
Ta có bảng biến thiên của hàm số:
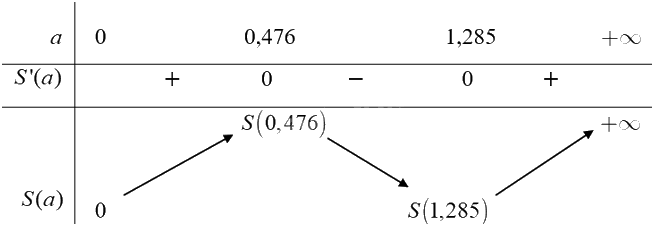
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(a) = S(1,285)\) tại \(a \approx 1,285\) hay \(\frac{D}{d} \approx 1,285\) suy ra \(d \approx \frac{D}{{1,285}}.\)
Bài 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề quan trọng như đạo hàm, tích phân, số phức và hình học không gian. Việc giải bài tập này không chỉ giúp học sinh nắm vững lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề, một yếu tố quan trọng để đạt kết quả cao trong các kỳ thi.
Bài 9 trang 37 thường bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống cụ thể. Các dạng bài tập phổ biến có thể kể đến như:
Để giải bài tập 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều:
Cho hàm số y = x3 - 3x2 + 2. Tìm cực đại và cực tiểu của hàm số.
Lời giải:
y' = 3x2 - 6x
y' = 0 ⇔ 3x2 - 6x = 0 ⇔ x = 0 hoặc x = 2
y'' = 6x - 6
y''(0) = -6 < 0 ⇒ Hàm số đạt cực đại tại x = 0, ymax = 2
y''(2) = 6 > 0 ⇒ Hàm số đạt cực tiểu tại x = 2, ymin = -2
Tính tích phân ∫01 x2 dx
Lời giải:
∫01 x2 dx = [x3/3]01 = 1/3 - 0 = 1/3
Tìm phần thực và phần ảo của số phức z = 2 + 3i
Lời giải:
Phần thực của z là Re(z) = 2
Phần ảo của z là Im(z) = 3
Để củng cố kiến thức và kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán khó.
Bài 9 trang 37 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về các chủ đề cơ bản của Toán 12. Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ có thể giải quyết bài tập một cách hiệu quả và đạt kết quả tốt nhất.