Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 36 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu sâu sắc kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các giải pháp học tập toàn diện và chất lượng.
Một nhà máy sản xuất một loại sản phẩm cho thị trường Mỹ. Biết rằng: - Chi phí cho các công việc hành chính chung của nhà máy là 90 đô la Mỹ (USD)/1 ngày. - Chi phí sản xuất là 0,09 USD/1 sản phẩm. - Các loại chi phí khác trong mỗi một ngày là \(\frac{{{x^2}}}{{10000}}\) (USD), trong đó \(x\) là số sản phẩm nhà máy sản xuất được trong ngày hôm đó. a) Tính tổng chi phí \(U(x)\) của mỗi một sản phẩm. b) Tìm \(x\) sao cho \(U(x)\) nhận giá trị nhỏ nhất.
Đề bài
Một nhà máy sản xuất một loại sản phẩm cho thị trường Mỹ. Biết rằng:
- Chi phí cho các công việc hành chính chung của nhà máy là 90 đô la Mỹ (USD)/1 ngày.
- Chi phí sản xuất là 0,09 USD/1 sản phẩm.
- Các loại chi phí khác trong mỗi một ngày là \(\frac{{{x^2}}}{{10000}}\) (USD), trong đó \(x\) là số sản phẩm nhà máy sản xuất được trong ngày hôm đó.
a) Tính tổng chi phí \(U(x)\) của mỗi một sản phẩm.
b) Tìm \(x\) sao cho \(U(x)\) nhận giá trị nhỏ nhất.
Phương pháp giải - Xem chi tiết
+) Tìm biểu thức biểu diễn chi phí công việc hành chính một ngày cho một sản phẩm.
+) Tìm biểu thức biểu diễn các loại chi phí khác cho một sản phẩm trong 1 ngày
+) \(U(x)\) là tổng các chi phí trong 1 ngày của một sản phẩm.
+) Ta sẽ đi tìm giá trị nhỏ nhất của hàm số \(U(x)\) trên \({\rm{[}}1; + \infty ).\)
Lời giải chi tiết
a) Chi phí cho các công việc hành chính chung trong một ngày của nhà máy cho mỗi sản phẩm là \(\frac{{90}}{x}\) (USD).
Các loại chi phí khác trong một ngày của nhà máy cho mỗi sản phẩm là \(\frac{x}{{10000}}\) (USD).
Tổng chi phí cho mỗi sản phẩm là \(U(x) = \frac{{90}}{x} + \frac{x}{{10000}}\) (USD).
b) Xét hàm số \(U(x) = \frac{{90}}{x} + \frac{x}{{10000}}\) trên \({\rm{[}}1; + \infty ).\)
Ta có \(U'(x) = - \frac{{90}}{{{x^2}}} + \frac{1}{{10000}}\).
Do đó \(U'(x) = 0 \Leftrightarrow - \frac{{90}}{{{x^2}}} + \frac{1}{{10000}} = 0 \Leftrightarrow {x^2} = 900000 \Leftrightarrow x \approx 948,7\) (do \(x > 0\)).
Bảng biến thiên hàm số:
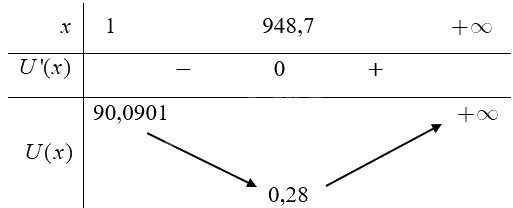
Căn cứ vào bảng biến thiên hàm số ta có \(\mathop {\min }\limits_{{\rm{[}}1; + \infty )} U(x) \approx 0,28\) tại \(x \approx 948,7.\)
Do \(x\) là số tự nhiên nên để chi phí nhỏ nhất khi \(x = 948\) hoặc \(x = 949.\)
Ta có \(U(948) \approx 0,2797367089\) và \(U(949) \approx 0,2797366702\) nên \(U(948) > U(949)\).
Vậy để \(U(x)\) nhận giá trị nhỏ nhất thì \(x = 949.\)
Bài 6 trang 36 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề quan trọng như đạo hàm, tích phân, số phức và hình học không gian. Việc nắm vững kiến thức này là nền tảng để các em giải quyết các bài toán phức tạp hơn trong kỳ thi THPT Quốc gia.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả các bài tập trong bài 6, các em cần nắm vững các kiến thức và kỹ năng sau:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5.
Ví dụ 2: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải:
f'(x) = 3x2 - 6x.
Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Xét dấu đạo hàm, ta thấy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em nên làm thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các đề thi thử. Ngoài ra, các em có thể tham khảo các tài liệu học tập trực tuyến trên giaitoan.edu.vn.
Để học tốt môn Toán 12, các em cần:
Bài 6 trang 36 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức và rèn luyện kỹ năng giải bài tập. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.