Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chuyên đề học tập của Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục 2, trang 14, 15 và 16, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những giải pháp học tập hiệu quả nhất.
a) Xét phép thử (T): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu (Omega ) của phép thử (T). b) Xét phép thử ({T_1}): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (({T_1}) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần
Trả lời câu hỏi Hoạt động 2 trang 14 Chuyên đề học tập Toán 12 Cánh diều
a) Xét phép thử \(T\): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu \(\Omega \) của phép thử \(T\).
b) Xét phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (\({T_1}\) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần thứ nhất).
Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung. Viết không gian mẫu \({\Omega _1}\) của phép thử \({T_1}\).
c) Trong phép thử lặp \({T_1}\) ta xét các biến cố:
\({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung”;
\({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung”;
\({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung”;
Phương pháp giải:
a,b: liệt kê các kết quả có thể xảy ra của phép thử.
c: Liệt kê các kết quả xảy ra của các biến cố \({A_0};{A_1};{A_2}\) từ đó tính xác suất xảy ra của các biến cố \({A_0};{A_1};{A_2}\).
Lời giải chi tiết:
a) Khi gieo đồng xu cân đối đồng chất thì sẽ có 2 trường hợp xảy ra là xuất hiện mặt sấp và xuất hiện mặt ngửa nên ta có không gian mẫu của phép thử \(T\) là: \(\Omega = \left\{ {S;\left. N \right\}} \right.\)
b) Khi gieo đồng xu 2 lần liên tiếp thì có thể xuất hiện 2 mặt sấp hoặc 2 mặt ngửa hoặc một mặt sấp một mặt ngửa nên ta có không gian mẫu của phép thử \({T_1}\) là: \({\Omega _1} = \{ SS;SN;NS;NN\} \)
c) Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
Ta có biến cố \({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung” nên ta có
\({A_0} = \{ NN\} \) \( \Rightarrow n({A_0}) = 1 \Rightarrow P({A_0}) = \frac{{n({A_0})}}{{n({\Omega _1})}} = \frac{1}{4}\)
Ta có biến cố \({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung” nên ta có
\(\) \({A_1} = \{ SN;NS\} \) \( \Rightarrow n({A_1}) = 2 \Rightarrow P({A_1}) = \frac{{n({A_1})}}{{n({\Omega _1})}} = \frac{2}{4} = \frac{1}{2}\)
Ta có biến cố \({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung” nên ta có
\({A_2} = \{ SS\} \) \( \Rightarrow n({A_2}) = 1 \Rightarrow P({A_2}) = \frac{{n({A_2})}}{{n({\Omega _1})}} = \frac{1}{4}\)
+) Với \(k = 0\) ta có \(C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4} = P({A_0})\)
+) Với \(k = 1\) ta có \(C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2} = P({A_1})\)
+) Với \(k = 2\) ta có \(C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4} = P({A_2})\)
Vậy \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}} = P({A_k})\)
Trả lời câu hỏi Hoạt động 2 trang 14 Chuyên đề học tập Toán 12 Cánh diều
a) Xét phép thử \(T\): “Tung một đồng xu cân đối và đồng chất một lần”. Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu. Viết không gian mẫu \(\Omega \) của phép thử \(T\).
b) Xét phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” (\({T_1}\) còn được gọi là phép thử lặp và việc tung một đồng xu hai lần liên tiếp một cách độc lập được hiểu là kết quả có thể xảy ra của lần thứ hai không phụ thuộc vào kết quả có thể xảy ra của tung lần thứ nhất).
Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung. Viết không gian mẫu \({\Omega _1}\) của phép thử \({T_1}\).
c) Trong phép thử lặp \({T_1}\) ta xét các biến cố:
\({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung”;
\({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung”;
\({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung”;
Phương pháp giải:
a,b: liệt kê các kết quả có thể xảy ra của phép thử.
c: Liệt kê các kết quả xảy ra của các biến cố \({A_0};{A_1};{A_2}\) từ đó tính xác suất xảy ra của các biến cố \({A_0};{A_1};{A_2}\).
Lời giải chi tiết:
a) Khi gieo đồng xu cân đối đồng chất thì sẽ có 2 trường hợp xảy ra là xuất hiện mặt sấp và xuất hiện mặt ngửa nên ta có không gian mẫu của phép thử \(T\) là: \(\Omega = \left\{ {S;\left. N \right\}} \right.\)
b) Khi gieo đồng xu 2 lần liên tiếp thì có thể xuất hiện 2 mặt sấp hoặc 2 mặt ngửa hoặc một mặt sấp một mặt ngửa nên ta có không gian mẫu của phép thử \({T_1}\) là: \({\Omega _1} = \{ SS;SN;NS;NN\} \)
c) Tính \(P({A_0})\); \(P({A_1})\); \(P({A_2})\)
Ta có biến cố \({A_0}\): “Mặt sấp không xuất hiện trong cả hai lần tung” nên ta có
\({A_0} = \{ NN\} \) \( \Rightarrow n({A_0}) = 1 \Rightarrow P({A_0}) = \frac{{n({A_0})}}{{n({\Omega _1})}} = \frac{1}{4}\)
Ta có biến cố \({A_1}\): “Mặt sấp xuất hiện một lần trong cả hai lần tung” nên ta có
\(\) \({A_1} = \{ SN;NS\} \) \( \Rightarrow n({A_1}) = 2 \Rightarrow P({A_1}) = \frac{{n({A_1})}}{{n({\Omega _1})}} = \frac{2}{4} = \frac{1}{2}\)
Ta có biến cố \({A_2}\): “Mặt sấp xuất hiện hai lần trong cả hai lần tung” nên ta có
\({A_2} = \{ SS\} \) \( \Rightarrow n({A_2}) = 1 \Rightarrow P({A_2}) = \frac{{n({A_2})}}{{n({\Omega _1})}} = \frac{1}{4}\)
+) Với \(k = 0\) ta có \(C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4} = P({A_0})\)
+) Với \(k = 1\) ta có \(C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2} = P({A_1})\)
+) Với \(k = 2\) ta có \(C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4} = P({A_2})\)
Vậy \(C_2^k.{\left( {\frac{1}{2}} \right)^k}.{\left( {\frac{1}{2}} \right)^{2 - k}} = P({A_k})\)
Trả lời câu hỏi Hoạt động 3 trang 16 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử lặp \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập”. Gọi \(X\) là số lần mặt ngửa xuất hiện sau hai lần tung.
Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\).
Phương pháp giải:
+) \(X\) là số lần xuất hiện mặt ngửa của phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” nên \(X\) sẽ nhận các giá trị 0;1;2
+) Ta sẽ tính các xác suất: \(P(X = 0);P(X = 1);P(X = 2)\)
Lời giải chi tiết:
Gieo một đồng xu cân đối đồng chất hai lần liên tiếp thì có các khả năng sau xảy ra : \(SS;SN;NS;NN\)
Gọi \({A_k}\) là biến cố “Mặt ngửa xuất hiện đúng \(k\) lần” \(k = 0;1;2\).
Vì xác suất xuất hiện mặt ngửa trong một lần tung là \(\frac{1}{2}\) nên ta áp dụng công thức Bernoulli với \(p = \frac{1}{2}\) và \(k = 0;1;2\) ta có:
\(P(X = 0) = P({A_0}) = C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4}\);
\(P(X = 1) = P({A_1}) = C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2}\)
\(P(X = 2) = P({A_2}) = C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4}\)
Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) như sau:
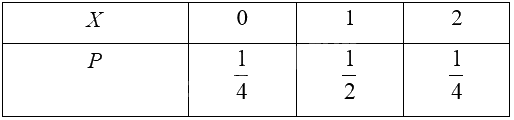
Trả lời câu hỏi Hoạt động 3 trang 16 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử lặp \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập”. Gọi \(X\) là số lần mặt ngửa xuất hiện sau hai lần tung.
Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\).
Phương pháp giải:
+) \(X\) là số lần xuất hiện mặt ngửa của phép thử \({T_1}\): “Tung một đồng xu cân đối và đồng chất hai lần liên tiếp một cách độc lập” nên \(X\) sẽ nhận các giá trị 0;1;2
+) Ta sẽ tính các xác suất: \(P(X = 0);P(X = 1);P(X = 2)\)
Lời giải chi tiết:
Gieo một đồng xu cân đối đồng chất hai lần liên tiếp thì có các khả năng sau xảy ra : \(SS;SN;NS;NN\)
Gọi \({A_k}\) là biến cố “Mặt ngửa xuất hiện đúng \(k\) lần” \(k = 0;1;2\).
Vì xác suất xuất hiện mặt ngửa trong một lần tung là \(\frac{1}{2}\) nên ta áp dụng công thức Bernoulli với \(p = \frac{1}{2}\) và \(k = 0;1;2\) ta có:
\(P(X = 0) = P({A_0}) = C_2^0.{\left( {\frac{1}{2}} \right)^0}.{\left( {\frac{1}{2}} \right)^{2 - 0}} = \frac{1}{4}\);
\(P(X = 1) = P({A_1}) = C_2^1.{\left( {\frac{1}{2}} \right)^1}.{\left( {\frac{1}{2}} \right)^{2 - 1}} = \frac{1}{2}\)
\(P(X = 2) = P({A_2}) = C_2^2.{\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{2}} \right)^{2 - 2}} = \frac{1}{4}\)
Ta có bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) như sau:
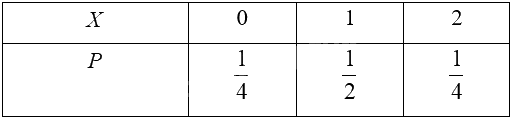
Mục 2 của Chuyên đề học tập Toán 12 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để giải quyết các bài tập một cách hiệu quả. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 14, 15 và 16, đồng thời phân tích các phương pháp tiếp cận phù hợp.
Trước khi đi vào giải bài tập, chúng ta cần xác định rõ nội dung chính của Mục 2. Thông thường, mục này sẽ giới thiệu các khái niệm mới, định lý quan trọng và các ví dụ minh họa. Việc hiểu rõ các khái niệm này sẽ giúp các em áp dụng chúng vào giải bài tập một cách chính xác.
Trong Mục 2, các em có thể gặp các dạng bài tập sau:
Bài 1: (Nêu đề bài tập 1 trang 14) ... (Giải chi tiết bài tập 1)
Bài 2: (Nêu đề bài tập 2 trang 14) ... (Giải chi tiết bài tập 2)
...(Tiếp tục giải các bài tập còn lại trên trang 14)
Bài 3: (Nêu đề bài tập 3 trang 15) ... (Giải chi tiết bài tập 3)
Bài 4: (Nêu đề bài tập 4 trang 15) ... (Giải chi tiết bài tập 4)
...(Tiếp tục giải các bài tập còn lại trên trang 15)
Bài 5: (Nêu đề bài tập 5 trang 16) ... (Giải chi tiết bài tập 5)
Bài 6: (Nêu đề bài tập 6 trang 16) ... (Giải chi tiết bài tập 6)
...(Tiếp tục giải các bài tập còn lại trên trang 16)
Để minh họa cho phương pháp giải, chúng ta sẽ xét bài tập (ví dụ một bài tập cụ thể). Lời giải chi tiết như sau:
(Giải chi tiết bài tập ví dụ)
Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục 2 trang 14, 15, 16 Chuyên đề học tập Toán 12 - Cánh diều. Chúc các em học tập tốt!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 14 | Dễ |
| Bài 2 | 14 | Trung bình |
| Bài 3 | 15 | Khó |