Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách nhanh chóng và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Có hai nhóm học sinh. Nhóm thứ nhất có 5 nam và 6 nữ. Nhóm thứ hai có 5 nam và 7 nữ. Từ mỗi nhóm học sinh, ta chọn ngẫu nhiên 1 học sinh. Gọi X là số học sinh nữ trong số 2 học sinh được chọn ra. a) Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc X. b) Tính kì vọng, phương sai của X.
Đề bài
Có hai nhóm học sinh. Nhóm thứ nhất có 5 nam và 6 nữ. Nhóm thứ hai có 5 nam và 7 nữ. Từ mỗi nhóm học sinh, ta chọn ngẫu nhiên 1 học sinh. Gọi X là số học sinh nữ trong số 2 học sinh được chọn ra.
a) Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc X.
b) Tính kì vọng, phương sai của X.
Phương pháp giải - Xem chi tiết
a) Gọi \(X = 0;X = 1;X = 2\)lần lượt là biến cố: “không có HS nữ được chọn”; “ có 1 HS nữ trong 2 HS được chọn”; “chọn được 2 HS nữ.”
Tính \(P(X = 0);P(X = 1);P(X = 2)\)
Lập bảng phân bố xác suất.
b) Áp dụng công thức:
Kì vọng: \(E(X) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\)
Phương sai: \(V(X) = {({x_1} - \mu )^2}{p_1} + {({x_2} - \mu )^2}{p_2} + ... + {({x_n} - \mu )^2}{p_n}\)
Lời giải chi tiết
a) X là biến ngẫu nhiên rời rạc và nhận giá trị trong tập \(\left\{ {0;1;2} \right\}\)
Ta có \(n(\Omega ) = C_{11}^1.C_{12}^1 = 132\)
+ Biến cố X=0 là biến cố :”Không có học sinh nữ được chọn.”
Suy ra \(n(X = 0) = C_5^1.C_5^1 = 25 \Rightarrow P(X = 0) = \frac{{25}}{{132}}.\)
+ Biến cố X=1 là biến cố :”Có 1 học sinh nữ trong số 2 hs được chọn.”
TH1: Nhóm 1 chọn được học sinh nữ, nhóm 2 chọn được học sinh nam
Suy ra có \(C_6^1.C_5^1 = 30\) cách chọn
TH2: Nhóm 1 chọn được học sinh nam, nhóm 2 chọn được học sinh nữ.
Suy ra có \(C_5^1.C_7^1 = 35\) cách chọn
Do đó \(P(X = 1) = \frac{{30 + 35}}{{132}} = \frac{{65}}{{132}}\)
+ Biến cố X=2 là biến cố :”Chọn được 2 HS nữ.”
Suy ra \(n(X = 2) = C_6^1.C_7^1 = 42 \Rightarrow P(X = 2) = \frac{{42}}{{132}}.\)
Bảng phân bố xác suất của X là:
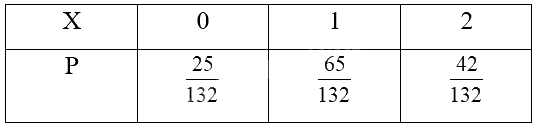
b) Có:
\(\begin{array}{l}E(X) = 0.\frac{{25}}{{132}} + 1.\frac{{65}}{{132}} + 2.\frac{{42}}{{132}} = \frac{{49}}{{132}}\\V(X) = {\left( {0 - \frac{{49}}{{132}}} \right)^2}.\frac{{25}}{{132}} + {\left( {1 - \frac{{49}}{{132}}} \right)^2}.\frac{{65}}{{132}} + {\left( {2 - \frac{{49}}{{132}}} \right)^2}.\frac{{42}}{{132}} \approx 0,49\end{array}\)
Bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về các chủ đề quan trọng như đạo hàm, tích phân, số phức và hình học không gian. Việc giải bài tập trong chuyên đề này không chỉ giúp học sinh hiểu sâu hơn về lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Bài 8 trang 12 bao gồm một loạt các bài tập khác nhau, từ các bài tập cơ bản đến các bài tập nâng cao, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Các bài tập thường xoay quanh các chủ đề sau:
Để giải bài tập bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diều một cách hiệu quả, học sinh cần:
Bài tập: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5.
Để học tốt Toán 12, các em nên:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải quyết vấn đề. Hy vọng rằng với những hướng dẫn và lời khuyên trên, các em sẽ giải bài tập một cách hiệu quả và đạt kết quả tốt nhất.