Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu sâu hơn về kiến thức Toán học.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác, dễ hiểu và đầy đủ.
Một cơ sở sản xuất đồ gỗ dự định sản xuất ba loại sả phẩm là bàn, ghế và tủ. Định mức sử dụng lao động, chi phí sản suất và giá bán mỗi sản phẩm mỗi loại ước tính trong Bảng 4: Biết rằng cơ sở sản xuất đó sử dụng không quá 500 ngày công, số tiền dành cho chi phí sản xuất không quá 40 triệu đồng và số ghế gấp sáu lần số bàn. Tính số sản phẩm mỗi loại cần phải sản xuất sao cho tổng doanh thu đạt được cao nhất.
Đề bài
Một cơ sở sản xuất đồ gỗ dự định sản xuất ba loại sả phẩm là bàn, ghế và tủ. Định mức sử dụng lao động, chi phí sản suất và giá bán mỗi sản phẩm mỗi loại ước tính trong Bảng 4:

Biết rằng cơ sở sản xuất đó sử dụng không quá 500 ngày công, số tiền dành cho chi phí sản xuất không quá 40 triệu đồng và số ghế gấp sáu lần số bàn. Tính số sản phẩm mỗi loại cần phải sản xuất sao cho tổng doanh thu đạt được cao nhất.
Phương pháp giải - Xem chi tiết
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết
Đổi 40 triệu đồng= 40 000 nghìn đồng.
Gọi \(x,y\) lần lượt là số chiếc bàn và số chiếc tủ cần sản cuất \((x \in N;y \in N)\)
Số chiếc ghế cần sản xuất là \(6x\) (chiếc)
Tổng doanh thu đạt được là \(T = 260x + 120.6x + 600y = 980x + 600y\) (nghìn đồng).
Số công lao động cần dùng là \(2x + 1.6x + 3y = 8x + 3y\) (ngày công)
Vì công lao động không vượt quá 500 ngày công nên ta có: \(8x + 3y \le 500.\)
Chi phí sản xuất các sản phẩm là \(100x + 40.6x + 250y = 340x + 250y\) (nghìn đồng)
Vì chi phí sản xuất không vượt quá 40 triệu đồng=40 000 nghìn đồng nên ta có \(340x + 250y \le 40000\) hay \(34x + 25y \le 4000\)
Vì cần thu được tổng doanh thu lớn nhất nên ta có bài toán quy hoạch tuyến tính: \(\left\{ \begin{array}{l}\max (T = 980x + 600y)\\8x + 3y \le 500\\34x + 25y \le 4000\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực):
\(\left\{ \begin{array}{l}8x + 3y \le 500\\34x + 25y \le 4000\\x \ge 0\\y \ge 0\end{array} \right.\) (II)
 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 980x + 600y\) khi \((x,y)\) thoả mãn hệ bất phương trình (II)
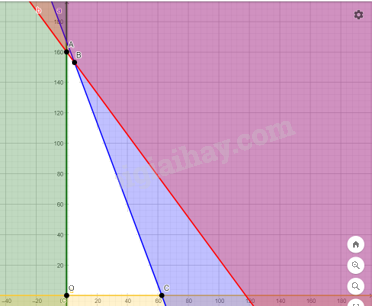
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);A(0;160);\) \(B\left( {\frac{{250}}{{49}};\frac{{7500}}{{49}}} \right);C(62,5;0)\).
Bước 2. Tính giá trị biểu thức \(T(x,y) = 980x + 600y\) tại các đỉnh của tứ giác OABC: \(T(0;0) = 0;T(0;160) = 96000;T\left( {\frac{{250}}{{49}};\frac{{7500}}{{49}}} \right) = \frac{{4745000}}{{49}};\) \(T(62,5;0) = 61250.\)
Bước 3. Ta đã biết biểu thức \(T = 980x + 600y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(0;160) = 96000.\)
Bước 4. Vì 0 và 160 là các số tự nhiên nên cặp số \((0;160)\) là nghiệm của bài toán (I).
Vậy chỉ cần sản xuất 160 chiếc tủ để tổng doanh thu đạt được là cao nhất.
Bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 4 trang 28 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 4 trang 28, chúng ta sẽ đi vào phân tích từng dạng bài tập cụ thể.
Để tìm đạo hàm của một hàm số, các em cần áp dụng các quy tắc tính đạo hàm đã học, bao gồm:
Ví dụ: Cho hàm số y = x2 + 2x - 1. Tìm đạo hàm y’.
Lời giải: y’ = 2x + 2
Khi giải phương trình, bất phương trình sử dụng đạo hàm, các em cần:
Ví dụ: Giải phương trình x3 - 3x + 2 = 0.
Lời giải: (Các bước giải chi tiết sẽ được trình bày đầy đủ)
Để khảo sát hàm số bằng đạo hàm, các em cần:
Ví dụ: Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải: (Các bước khảo sát chi tiết sẽ được trình bày đầy đủ)
Các bài toán tối ưu hóa thường yêu cầu tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trên một khoảng cho trước. Để giải các bài toán này, các em cần:
Ví dụ: Tìm giá trị lớn nhất của hàm số y = -x2 + 4x - 3 trên khoảng [0; 2].
Lời giải: (Các bước giải chi tiết sẽ được trình bày đầy đủ)
Để giải bài tập về đạo hàm một cách hiệu quả, các em cần:
Bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả.