Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 4 trang 36 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và áp dụng kiến thức vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của cá khi nước đứng yên là \(v\) (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức \(E(v) = c{v^3}t\) Trong đó \(c\) là một hằng số, \(E\) được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Đề bài
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300 km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của cá khi nước đứng yên là \(v\) (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức
\(E(v) = c{v^3}t\)
Trong đó \(c\) là một hằng số, \(E\) được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Phương pháp giải - Xem chi tiết
+) Biểu diễn vận tốc của cá hồi khi bơi ngược dòng là \(v - 6\) (km/h)
+) Từ đó ta tìm thời gian cá hồi bơi ngược dòng trong quãng đường 300 km là \(\frac{{300}}{{v - 6}}\)(giờ)
+) Từ đó thay thời gian bơi vào biểu thức tính năng lượng tiêu hao\(E(v) = c{v^3}t\) ta sẽ được một hàm số chỉ có ẩn \(v\)
+) Xét hàm số ấn \(v\), yêu cầu bài toán tương đương với việc tìm giá trị nhỏ nhất của hàm số này.
Lời giải chi tiết
Vận tốc của con cá hồi khi bơi ngược dòng là \(v - 6\) (km/h).
Thời gian để con cá hồi đó bơi ngược dòng 300 km là \(\frac{{300}}{{v - 6}}\) (giờ).
Năng lượng tiêu hao của cá để vượt quãng đường 300 km là
\(E(v) = c{v^3}.\frac{{300}}{{v - 6}} = 300c.\frac{{{v^3}}}{{v - 6}}\) (jun)
Xét hàm số \(E(v) = 300c.\frac{{{v^3}}}{{v - 6}},\) \(v > 6.\)
Ta có \(E'(v) = 300c.\frac{{3{v^2}(v - 6) - {v^3}}}{{{{(v - 6)}^2}}} = 300c.\frac{{2{v^3} - 18{v^2}}}{{{{(v - 6)}^2}}}.\)
Do đó \(E'(v) = 0 \Leftrightarrow v = 0\)(không thoả mãn) hoặc \(v = 9\) (thoả mãn).
Ta có bảng biến thiên:
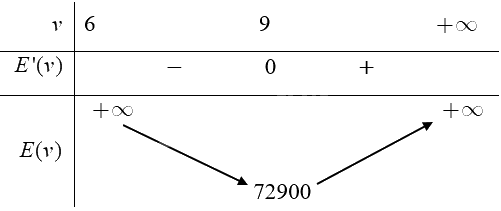
Căn cứ vào bảng biến thiên, ta có \(\mathop {\min }\limits_{(6; + \infty )} E(v) = E(9) = 72900\) tại \(v = 9.\)
Vậy vận tốc bơi của cá hồi khi nước đứng yên để năng lượng tiêu hao là ít nhất là 9 km/h.
Bài 4 trang 36 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, tìm cực trị, và khảo sát sự biến thiên của hàm số. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là yếu tố then chốt để giải quyết bài toán này một cách hiệu quả.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 4 trang 36, học sinh cần xác định hàm số cần khảo sát, các điểm không xác định, và các khoảng đơn điệu của hàm số. Ngoài ra, cần chú ý đến các điều kiện ràng buộc của bài toán để đảm bảo tính chính xác của lời giải.
Để giải bài 4 trang 36 Chuyên đề học tập Toán 12 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:
Giả sử hàm số cần khảo sát là f(x) = x^3 - 3x^2 + 2. Ta thực hiện các bước sau:
Khi giải bài tập về đạo hàm, học sinh cần chú ý các điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 4 trang 36 Chuyên đề học tập Toán 12 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến đạo hàm. Bằng cách nắm vững các khái niệm, phương pháp giải, và lưu ý quan trọng, học sinh có thể tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.