Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách Chuyên đề học tập Toán 12 Cánh diều. Mục 1 trang 13 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Xét phép thử (T): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi (X) là số lần bắn trúng mục tiêu. Khi đó, (X) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp ({ 0,1} ). Giả sử (P(X = 1) = p(0 < p < 1)). Suy ra (P(X = 0) = 1 - p). Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc (X).
Trả lời câu hỏi Hoạt động 1 trang 13 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử \(T\): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi \(X\) là số lần bắn trúng mục tiêu. Khi đó, \(X\) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp \(\{ 0,1\} \).
Giả sử \(P(X = 1) = p(0 < p < 1)\). Suy ra \(P(X = 0) = 1 - p\).
Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc \(X\).
Phương pháp giải:
+ Lập bảng phân bố xác suất với \(X\) nhận các giá trị 0,1
+ \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\)
Lời giải chi tiết:
Ta có \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\). Vậy biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
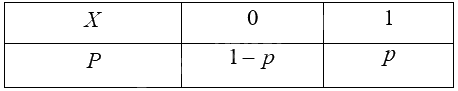
Trả lời câu hỏi Hoạt động 1 trang 13 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử \(T\): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi \(X\) là số lần bắn trúng mục tiêu. Khi đó, \(X\) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp \(\{ 0,1\} \).
Giả sử \(P(X = 1) = p(0 < p < 1)\). Suy ra \(P(X = 0) = 1 - p\).
Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc \(X\).
Phương pháp giải:
+ Lập bảng phân bố xác suất với \(X\) nhận các giá trị 0,1
+ \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\)
Lời giải chi tiết:
Ta có \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\). Vậy biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
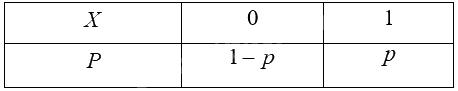
Mục 1 trang 13 trong Chuyên đề học tập Toán 12 Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như các khái niệm về đạo hàm, tích phân, hoặc các bài toán về hình học không gian. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để giải quyết thành công các bài tập trong mục này.
Giả sử Mục 1 trang 13 tập trung vào việc tính đạo hàm của các hàm số lượng giác. Các kiến thức cần nắm vững bao gồm:
Để giải các bài tập trong Mục 1 trang 13, bạn cần:
Bài tập: Tính đạo hàm của hàm số y = sin(2x).
Lời giải:
Sử dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x) * (2x)' = 2cos(2x)
Ngoài việc giải các bài tập trong sách giáo khoa, bạn có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong các lĩnh vực khác như vật lý, kinh tế, và kỹ thuật. Điều này sẽ giúp bạn hiểu sâu hơn về tầm quan trọng của đạo hàm trong cuộc sống.
Giải mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh diều đòi hỏi sự nắm vững kiến thức lý thuyết và kỹ năng giải quyết vấn đề. Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải các bài tập và đạt kết quả tốt trong môn Toán.