Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.9 trang 37 trong Chuyên đề học tập Toán 10 – Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải bài tập Toán 10 một cách logic và dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Sử dụng tam giác Pascal, viết khai triển:
Đề bài
Sử dụng tam giác Pascal, viết khai triển:
a) \({(x - 1)^5}\)
b) \({(2x - 3y)^4}\)
Phương pháp giải - Xem chi tiết
Tam giác Pascal
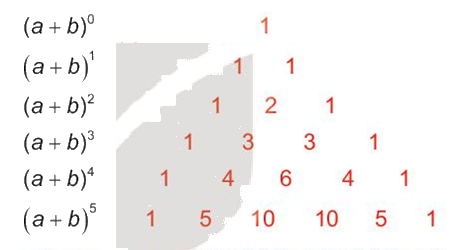
Lời giải chi tiết
a)
\(\begin{array}{l}{(x - 1)^5} = {x^5} + 5.{x^4}.( - 1) + 10.{x^3}.{( - 1)^2} + 10.{x^2}.{( - 1)^3} + 5x.{( - 1)^4} + {( - 1)^5}\\ = {x^5} - 5{x^4} + 10{x^3} + 10{x^2} + 5x - 1\end{array}\)
b)
\(\begin{array}{l}{(2x - 3y)^4} = {\left( {2x} \right)^4} + 4{\left( {2x} \right)^3}.( - 3y) + 6{\left( {2x} \right)^2}.{( - 3y)^2} + 4\left( {2x} \right).{( - 3y)^3} + {( - 3y)^4}\\ = 16{x^4} - 96{x^3}y + 216{x^2}{y^2} - 216x{y^3} + 81{y^4}\end{array}\)
Bài 2.9 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản như:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta tính toán các giá trị liên quan đến vectơ, chứng minh một đẳng thức vectơ hoặc giải một bài toán hình học sử dụng vectơ.
Để giải bài 2.9 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức, chúng ta sẽ thực hiện theo các bước sau:
Giả sử đề bài yêu cầu chúng ta tính độ dài của vectơ a = (2; -3). Chúng ta sẽ thực hiện như sau:
Độ dài của vectơ a được tính bằng công thức: |a| = √(x² + y²), trong đó x và y là tọa độ của vectơ a.
Thay x = 2 và y = -3 vào công thức, ta được: |a| = √(2² + (-3)²) = √(4 + 9) = √13.
Vậy độ dài của vectơ a là √13.
Khi giải bài tập về vectơ, chúng ta cần lưu ý một số điều sau:
Để củng cố kiến thức về vectơ, bạn có thể làm thêm một số bài tập tương tự sau:
Bài 2.9 trang 37 Chuyên đề học tập Toán 10 – Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |