Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 Chuyên đề học tập - Kết nối tri thức. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 42, 43, 44, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho Elip có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) và độ dài trục lớn bằng 2a và điểm \(M(x;y)\).
Cho Elip có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) và độ dài trục lớn bằng 2a và điểm \(M(x;y)\).
a) Tính \(M{F_1}^2 - M{F_2}^2\)
b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)), tính \(M{F_1} - M{F_2},M{F_1},M{F_2}.\)
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {M{F_1}} ( - c - x; - y);\overrightarrow {M{F_2}} (c - x; - y)\)
\( \Rightarrow M{F_1}^2 = {( - c - x)^2} + {( - y)^2};M{F_2}^2 = {(c - x)^2} + {( - y)^2}\)
\( \Rightarrow M{F_1}^2 - M{F_2}^2 = {( - c - x)^2} - {(c - x)^2} = 4cx\)
b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} - M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} + M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a - \frac{{2c}}{a}x}}{2} = a - \frac{c}{a}x\end{array}\)
Cho elip \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\), điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_1}( - c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc elip, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c\) khi M trùng \({A_1}( - a;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c\) khi M trùng \({A_2}(a;0)\)
Lời giải chi tiết:
Ta có: \({a^2} = 36,{b^2} = 20 \Rightarrow a = 6,b = 2\sqrt 5 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 4\)
Xét tiêu điểm \({F_1}( - 4;0)\)
\(M{F_1}\) nhỏ nhất bằng \(a - c = 2\) khi M trùng \({A_1}( - 6;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c = 10\) khi M trùng \({A_2}(6;0)\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\). Tìm tâm sai và các đường chuẩn của elip. Tính các bán kính qua tiêu của điểm M thuộc elip và có hoành độ bằng -2.
Phương pháp giải:
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} - {b^2}} \)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).
+ Bán kính qua tiêu của M (x; y): \(M{F_1} = a + ex,\;M{F_2} = a - ex.\)
Lời giải chi tiết:
Ta có phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\).
\( \Rightarrow a = 6,b = 5,c = \sqrt {{a^2} - {b^2}} = \sqrt {11} \)
+ Tâm sai của elip: \(e = \frac{{\sqrt {11} }}{6}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{{36\sqrt {11} }}{{11}}\) và \({\Delta _2}:x = \frac{{36\sqrt {11} }}{{11}}\).
+ Bán kính qua tiêu của M (-2; y): \(M{F_1} = 6 + \frac{{\sqrt {11} }}{6}.( - 2) = 6 - \frac{{\sqrt {11} }}{3},\;M{F_2} = 6 - \frac{{\sqrt {11} }}{6}.( - 2) = 6 + \frac{{\sqrt {11} }}{3}.\)
Mặt trăng chuyển động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu điểm. Các khoảng cách lớn nhất và nhỏ nhất từ các vị trí của Mặt Trăng đến tâm Trái Đất tương ứng là 400 000 km và 363 000 km (theo nssdc.gsfc.nasa.gov). Tìm tâm sai của quỹ đạo elip.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_1}( - c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc elip, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c\) khi M trùng \({A_1}( - a;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c\) khi M trùng \({A_2}(a;0)\)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
Lời giải chi tiết:
Gọi PTCT của quỹ đạo hình elip đó là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\),
Giả sử Trái Đất là tiêu điểm \({F_1}( - c;0)\).
Điểm M bất kì thuộc elip là vị trí của Mặt trăng trong quỹ đạo, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c = 363\;000\)
\(M{F_1}\) lớn nhất bằng \(a + c = 400\;000\)
\( \Rightarrow a = 381500,\;c = 18500\)
\( \Rightarrow \)Tâm sai của elip là: \(e = \frac{{18500}}{{381500}} = \frac{{37}}{{763}}.\)
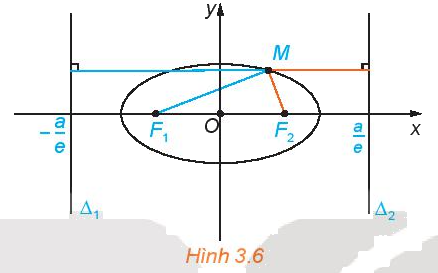
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} - {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = - \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).
Với điểm M (x; y) thuộc elip, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.
Phương pháp giải:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
\(M{F_1} = a + \frac{c}{a}x = \frac{{{a^2} + cx}}{a};\;\;M{F_2} = a - \frac{c}{a}x = \frac{{{a^2} - cx}}{a}\)
\(d(M,{\Delta _1}) = \frac{{{a^2}}}{c} + x = \frac{{{a^2} + cx}}{c}\)
\(d(M,{\Delta _2}) = \frac{{{a^2}}}{c} - x = \frac{{{a^2} - cx}}{c}\)
\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{{a^2} + cx}}{a}:\frac{{{a^2} + cx}}{c} = \frac{c}{a}\) ; \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{{a^2} - cx}}{a}:\frac{{{a^2} - cx}}{c} = \frac{c}{a}\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)
Với thông tin đưa ra trong tình huống mở đầu, lập phương trình chính tắc của elip quỹ đạo của Trái Đất, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^6}km\) trên thực tế.

Phương pháp giải:
Coi tâm mặt trời là gốc tọa độ trong PTCT \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(b \le OM \le a\)
\(\begin{array}{l}OM = b \Leftrightarrow M \equiv {B_1}\left( {0; - b} \right);{B_2}\left( {0;b} \right).\\OM = a \Leftrightarrow M \equiv {A_1}\left( { - a;0} \right);{A_2}\left( {a;0} \right).\end{array}\)
Lời giải chi tiết:
Coi tâm mặt trời là gốc tọa độ O.
Gọi PTCT của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
M là vị trí của Trái Đất, rõ ràng \(M \in (E)\)
Vì \(b \le OM \le a\) nên \(a = {152.10^6};b = {147.10^6}\)
\( \Rightarrow \) Phương trình chính tắc của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{{23104.10}^{12}}}} + \frac{{{y^2}}}{{{{21609.10}^{12}}}} = 1\)
Cho Elip có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\) và độ dài trục lớn bằng 2a và điểm \(M(x;y)\).
a) Tính \(M{F_1}^2 - M{F_2}^2\)
b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)), tính \(M{F_1} - M{F_2},M{F_1},M{F_2}.\)
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {M{F_1}} ( - c - x; - y);\overrightarrow {M{F_2}} (c - x; - y)\)
\( \Rightarrow M{F_1}^2 = {( - c - x)^2} + {( - y)^2};M{F_2}^2 = {(c - x)^2} + {( - y)^2}\)
\( \Rightarrow M{F_1}^2 - M{F_2}^2 = {( - c - x)^2} - {(c - x)^2} = 4cx\)
b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} - M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} + M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a - \frac{{2c}}{a}x}}{2} = a - \frac{c}{a}x\end{array}\)
Cho elip \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\), điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_1}( - c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc elip, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c\) khi M trùng \({A_1}( - a;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c\) khi M trùng \({A_2}(a;0)\)
Lời giải chi tiết:
Ta có: \({a^2} = 36,{b^2} = 20 \Rightarrow a = 6,b = 2\sqrt 5 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 4\)
Xét tiêu điểm \({F_1}( - 4;0)\)
\(M{F_1}\) nhỏ nhất bằng \(a - c = 2\) khi M trùng \({A_1}( - 6;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c = 10\) khi M trùng \({A_2}(6;0)\)
Với thông tin đưa ra trong tình huống mở đầu, lập phương trình chính tắc của elip quỹ đạo của Trái Đất, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^6}km\) trên thực tế.

Phương pháp giải:
Coi tâm mặt trời là gốc tọa độ trong PTCT \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Với M bất kì thuộc Elip, ta luôn có: \(b \le OM \le a\)
\(\begin{array}{l}OM = b \Leftrightarrow M \equiv {B_1}\left( {0; - b} \right);{B_2}\left( {0;b} \right).\\OM = a \Leftrightarrow M \equiv {A_1}\left( { - a;0} \right);{A_2}\left( {a;0} \right).\end{array}\)
Lời giải chi tiết:
Coi tâm mặt trời là gốc tọa độ O.
Gọi PTCT của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
M là vị trí của Trái Đất, rõ ràng \(M \in (E)\)
Vì \(b \le OM \le a\) nên \(a = {152.10^6};b = {147.10^6}\)
\( \Rightarrow \) Phương trình chính tắc của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{{23104.10}^{12}}}} + \frac{{{y^2}}}{{{{21609.10}^{12}}}} = 1\)
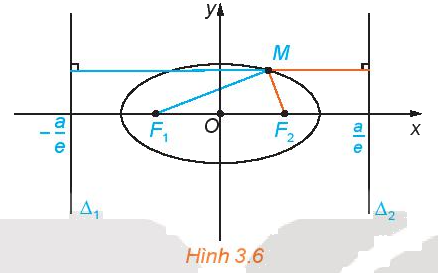
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} - {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = - \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).
Với điểm M (x; y) thuộc elip, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.
Phương pháp giải:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
\(M{F_1} = a + \frac{c}{a}x = \frac{{{a^2} + cx}}{a};\;\;M{F_2} = a - \frac{c}{a}x = \frac{{{a^2} - cx}}{a}\)
\(d(M,{\Delta _1}) = \frac{{{a^2}}}{c} + x = \frac{{{a^2} + cx}}{c}\)
\(d(M,{\Delta _2}) = \frac{{{a^2}}}{c} - x = \frac{{{a^2} - cx}}{c}\)
\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{{a^2} + cx}}{a}:\frac{{{a^2} + cx}}{c} = \frac{c}{a}\) ; \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{{a^2} - cx}}{a}:\frac{{{a^2} - cx}}{c} = \frac{c}{a}\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\). Tìm tâm sai và các đường chuẩn của elip. Tính các bán kính qua tiêu của điểm M thuộc elip và có hoành độ bằng -2.
Phương pháp giải:
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} - {b^2}} \)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).
+ Bán kính qua tiêu của M (x; y): \(M{F_1} = a + ex,\;M{F_2} = a - ex.\)
Lời giải chi tiết:
Ta có phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\).
\( \Rightarrow a = 6,b = 5,c = \sqrt {{a^2} - {b^2}} = \sqrt {11} \)
+ Tâm sai của elip: \(e = \frac{{\sqrt {11} }}{6}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{{36\sqrt {11} }}{{11}}\) và \({\Delta _2}:x = \frac{{36\sqrt {11} }}{{11}}\).
+ Bán kính qua tiêu của M (-2; y): \(M{F_1} = 6 + \frac{{\sqrt {11} }}{6}.( - 2) = 6 - \frac{{\sqrt {11} }}{3},\;M{F_2} = 6 - \frac{{\sqrt {11} }}{6}.( - 2) = 6 + \frac{{\sqrt {11} }}{3}.\)
Mặt trăng chuyển động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu điểm. Các khoảng cách lớn nhất và nhỏ nhất từ các vị trí của Mặt Trăng đến tâm Trái Đất tương ứng là 400 000 km và 363 000 km (theo nssdc.gsfc.nasa.gov). Tìm tâm sai của quỹ đạo elip.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_1}( - c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc elip, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c\) khi M trùng \({A_1}( - a;0)\)
\(M{F_1}\) lớn nhất bằng \(a + c\) khi M trùng \({A_2}(a;0)\)
+ Tâm sai của elip: \(e = \frac{c}{a}\)
Lời giải chi tiết:
Gọi PTCT của quỹ đạo hình elip đó là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\),
Giả sử Trái Đất là tiêu điểm \({F_1}( - c;0)\).
Điểm M bất kì thuộc elip là vị trí của Mặt trăng trong quỹ đạo, khi đó:
\(M{F_1}\) nhỏ nhất bằng \(a - c = 363\;000\)
\(M{F_1}\) lớn nhất bằng \(a + c = 400\;000\)
\( \Rightarrow a = 381500,\;c = 18500\)
\( \Rightarrow \)Tâm sai của elip là: \(e = \frac{{18500}}{{381500}} = \frac{{37}}{{763}}.\)
Mục 2 của Chuyên đề học tập Toán 10 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Việc giải các bài tập trang 42, 43, 44 không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề, một kỹ năng vô cùng quan trọng trong học tập và cuộc sống.
Các bài tập trang 42 thường xoay quanh việc vận dụng các định nghĩa, tính chất cơ bản của chủ đề đang học. Ví dụ, nếu chủ đề là về vectơ, các bài tập có thể yêu cầu tính độ dài vectơ, tìm tọa độ vectơ, hoặc chứng minh các đẳng thức vectơ.
Trang 43 thường chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải kết hợp nhiều kiến thức khác nhau để giải quyết. Các bài tập này có thể liên quan đến việc giải phương trình, bất phương trình, hoặc chứng minh các bài toán hình học.
Các bài tập trang 44 thường là các bài tập tổng hợp, giúp học sinh ôn lại toàn bộ kiến thức đã học trong mục 2. Các bài tập này có thể có nhiều dạng khác nhau, đòi hỏi học sinh phải có khả năng phân tích và lựa chọn phương pháp giải phù hợp.
| Bài tập | Lời giải |
|---|---|
| Bài 7 | (Nêu rõ yêu cầu bài tập và lời giải chi tiết) |
| Bài 8 | (Nêu rõ yêu cầu bài tập và lời giải chi tiết) |
| Bài 9 | (Nêu rõ yêu cầu bài tập và lời giải chi tiết) |
Để giải các bài tập Toán 10 - Kết nối tri thức một cách hiệu quả, các em cần:
Học Toán 10 đòi hỏi sự kiên trì và nỗ lực. Các em nên:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải toán hiệu quả được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 42, 43, 44 Chuyên đề học tập Toán 10 - Kết nối tri thức. Chúc các em học tập tốt!