Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 49, 50, 51, 52 Chuyên đề học tập Toán 10 - Kết nối tri thức. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho điểm (M({x_0};{y_0}))thuộc hypebol có hai tiêu điểm ({F_1}( - c;0),{F_2}(c;0)), độ dài trục thực bằng 2a.
Cho điểm \(M({x_0};{y_0})\)thuộc hypebol có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\), độ dài trục thực bằng 2a.
a) Tính \(M{F_1}^2 - M{F_2}^2\)
b) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\), tức là,\(M{F_1} - M{F_2} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
c) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\), tức là,\(M{F_2} - M{F_1} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {M{F_1}} ( - c - {x_0}; - {y_0});\overrightarrow {M{F_2}} (c - {x_0}; - {y_0})\)
\( \Rightarrow M{F_1}^2 = {( - c - {x_0})^2} + {( - {y_0})^2};M{F_2}^2 = {(c - {x_0})^2} + {( - {y_0})^2}\)
\( \Rightarrow M{F_1}^2 - M{F_2}^2 = {( - c - {x_0})^2} - {(c - {x_0})^2} = 4c{x_0}\)
b) Khi điểm M \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) (\(M{F_1} - M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\frac{{2c}}{a}{x_0} + 2a}}{2} = a + \frac{c}{a}{x_0}\\M{F_2} = \frac{{\frac{{2c}}{a}{x_0} - 2a}}{2} = - a + \frac{c}{a}{x_0}\end{array}\)
c) Khi điểm \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) (\(M{F_2} - M{F_1} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = - \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) - 2a}}{2} = - a - \frac{c}{a}{x_0}\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) + 2a}}{2} = a - \frac{c}{a}{x_0}\end{array}\)
Cho hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\). Điểm M nào thuộc hypebol mà có độ dài bán kính qua tiêu \(M{F_2}\) nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm
Phương pháp giải:
\(M{F_2}\) nhỏ nhất bằng \(c - a\) khi M trùng đỉnh \({A_2}(a;0)\)
Lời giải chi tiết:
Xét hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\), ta có:
\(a = 1,b = \sqrt 3 ,c = 2\).
\( \Rightarrow M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(1;0)\)
Khi đó, \(M{F_1} = \left| {1 + \frac{2}{1}.1} \right| = 3.\)
Hiệu độ dài hai bán kính qua tiêu của một điểm thuộc hypebol có mối quan hệ gì với độ dài trục thực?
Lời giải chi tiết:
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) thì \(M{F_1} - M{F_2} = 2a\)
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) thì \(M{F_2} - M{F_1} = 2a\)
\( \Rightarrow \left| {M{F_1} - M{F_2}} \right| = 2a\)
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng \(6\sqrt 3 \). Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Phương pháp giải:
Độ dài trục thực bằng \(2a\), độ dài trục ảo bằng \(2b\).
Với \(M({x_0};{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {a + \frac{c}{a}{x_0}} \right|;M{F_2} = \left| {a - \frac{c}{a}{x_0}} \right|\)
Lời giải chi tiết:
Độ dài trục thực bằng \(2a = 6 \Rightarrow a = 3.\)
Độ dài trục ảo bằng \(2b = 6\sqrt 3 \Rightarrow b = 3\sqrt 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = 6\).
Với \(M(9;{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {3 + \frac{6}{3}.9} \right| = 21;M{F_2} = \left| {3 - \frac{6}{3}.9} \right| = 15.\)
Trong mặt phẳng tọa độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai \(e = 2\) và một đường chuẩn là \(x = 8\). Lập phương trình chính tắc của (H).
Phương pháp giải:
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} + {b^2}} \)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).
Lời giải chi tiết:
Phương trình chính tắc của hypebol có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
Vì \(a,c > 0\) nên \(e > 0\)
+ Đường chuẩn: \({\Delta _2}:x = 8 = \frac{a}{2} \Rightarrow a = 16\)
+ Tâm sai của hypebol: \(e = 2 \Rightarrow \frac{c}{{16}} = 2 \Rightarrow c = 32 \Rightarrow b = 16\sqrt 3 \)
Phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{256}} - \frac{{{y^2}}}{{768}} = 1\).
Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt trời là \({3.10^8}\) km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15). Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^8}\) km trên thực tế.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_2}(c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc hypebol, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(a;0)\)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
Lời giải chi tiết:
\({3.10^8}\) km = 3 đơn vị.
Gọi PTCT của quỹ đạo hình hypebol đó là: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\),
Giả sử Mặt trời là tiêu điểm \({F_2}( - c;0)\).
Điểm M bất kì thuộc hypebol là vị trí của sao chổi trong quỹ đạo, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 3\) khi M trùng đỉnh \({A_2}(a;0)\)
Tâm sai của hypebol là: \(e = \frac{c}{a} = 3,6 \Rightarrow c = 3,6a\)
\( \Rightarrow 2,6a = 3 \Leftrightarrow a = \frac{{15}}{{13}},\;c = \frac{{54}}{{13}} \Rightarrow {b^2} = \frac{{207}}{{13}}\)
\( \Rightarrow \)PTCT của hypebol là: \(\frac{{169{x^2}}}{{225}} - \frac{{13{y^2}}}{{207}} = 1\),
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} - {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = - \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).
Với điểm M (x; y) thuộc hypebol, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.
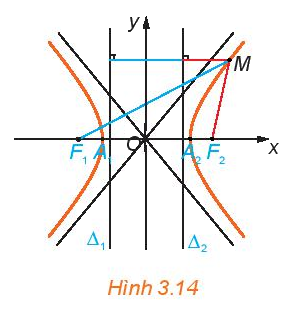
Phương pháp giải:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
Ta có:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;\;\;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
\(d(M,{\Delta _1}) = \left| {x - \left( { - \frac{{{a^2}}}{c}} \right)} \right| = \left| {x + \frac{{{a^2}}}{c}} \right|\); \(d(M,{\Delta _2}) = \left| {x - \frac{{{a^2}}}{c}} \right|\)
\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \left| {\frac{{{a^2} + cx}}{a}} \right|:\left| {\frac{{{a^2} + cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\) ;
\(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \left| {\frac{{{a^2} - cx}}{a}} \right|:\left| {\frac{{{a^2} - cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)
Cho điểm \(M({x_0};{y_0})\)thuộc hypebol có hai tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\), độ dài trục thực bằng 2a.
a) Tính \(M{F_1}^2 - M{F_2}^2\)
b) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\), tức là,\(M{F_1} - M{F_2} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
c) Giả sử \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\), tức là,\(M{F_2} - M{F_1} = 2a\). Tính \(M{F_1} + M{F_2},M{F_1},M{F_2}.\)
Lời giải chi tiết:
a) Tính \(M{F_1}^2 - M{F_2}^2\)
Ta có: \(\overrightarrow {M{F_1}} ( - c - {x_0}; - {y_0});\overrightarrow {M{F_2}} (c - {x_0}; - {y_0})\)
\( \Rightarrow M{F_1}^2 = {( - c - {x_0})^2} + {( - {y_0})^2};M{F_2}^2 = {(c - {x_0})^2} + {( - {y_0})^2}\)
\( \Rightarrow M{F_1}^2 - M{F_2}^2 = {( - c - {x_0})^2} - {(c - {x_0})^2} = 4c{x_0}\)
b) Khi điểm M \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) (\(M{F_1} - M{F_2} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\frac{{2c}}{a}{x_0} + 2a}}{2} = a + \frac{c}{a}{x_0}\\M{F_2} = \frac{{\frac{{2c}}{a}{x_0} - 2a}}{2} = - a + \frac{c}{a}{x_0}\end{array}\)
c) Khi điểm \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) (\(M{F_2} - M{F_1} = 2a\)),
\(\begin{array}{l}M{F_1} + M{F_2} = \frac{{M{F_1}^2 - M{F_2}^2}}{{M{F_1} - M{F_2}}} = - \frac{{2c}}{a}{x_0}\\M{F_1} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) - 2a}}{2} = - a - \frac{c}{a}{x_0}\\M{F_2} = \frac{{\left( { - \frac{{2c}}{a}{x_0}} \right) + 2a}}{2} = a - \frac{c}{a}{x_0}\end{array}\)
Hiệu độ dài hai bán kính qua tiêu của một điểm thuộc hypebol có mối quan hệ gì với độ dài trục thực?
Lời giải chi tiết:
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_2}(a;0)\) thì \(M{F_1} - M{F_2} = 2a\)
Nếu \(M({x_0};{y_0})\) thuộc nhánh chứa đỉnh \({A_1}( - a;0)\) thì \(M{F_2} - M{F_1} = 2a\)
\( \Rightarrow \left| {M{F_1} - M{F_2}} \right| = 2a\)
Cho hypebol có độ dài trục thực bằng 6, độ dài trục ảo bằng \(6\sqrt 3 \). Tính độ dài hai bán kính qua tiêu của một điểm M thuộc hypebol và có hoành độ bằng 9.
Phương pháp giải:
Độ dài trục thực bằng \(2a\), độ dài trục ảo bằng \(2b\).
Với \(M({x_0};{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {a + \frac{c}{a}{x_0}} \right|;M{F_2} = \left| {a - \frac{c}{a}{x_0}} \right|\)
Lời giải chi tiết:
Độ dài trục thực bằng \(2a = 6 \Rightarrow a = 3.\)
Độ dài trục ảo bằng \(2b = 6\sqrt 3 \Rightarrow b = 3\sqrt 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = 6\).
Với \(M(9;{y_0})\) thuộc hypebol ta có:
\(M{F_1} = \left| {3 + \frac{6}{3}.9} \right| = 21;M{F_2} = \left| {3 - \frac{6}{3}.9} \right| = 15.\)
Cho hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\). Điểm M nào thuộc hypebol mà có độ dài bán kính qua tiêu \(M{F_2}\) nhỏ nhất? Tính khoảng cách từ điểm đó tới các tiêu điểm
Phương pháp giải:
\(M{F_2}\) nhỏ nhất bằng \(c - a\) khi M trùng đỉnh \({A_2}(a;0)\)
Lời giải chi tiết:
Xét hypebol \(\frac{{{x^2}}}{1} - \frac{{{y^2}}}{3} = 1\) với hai tiêu điểm \({F_1}( - 2;0),{F_2}(2;0)\), ta có:
\(a = 1,b = \sqrt 3 ,c = 2\).
\( \Rightarrow M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(1;0)\)
Khi đó, \(M{F_1} = \left| {1 + \frac{2}{1}.1} \right| = 3.\)
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} - {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = - \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).
Với điểm M (x; y) thuộc hypebol, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.
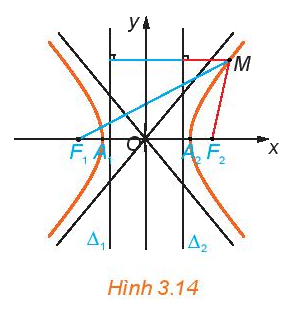
Phương pháp giải:
\(M{F_1} = a + \frac{c}{a}x;M{F_2} = a - \frac{c}{a}x\)
Lời giải chi tiết:
Ta có:
\(M{F_1} = \left| {a + \frac{c}{a}x} \right|;\;\;M{F_2} = \left| {a - \frac{c}{a}x} \right|\)
\(d(M,{\Delta _1}) = \left| {x - \left( { - \frac{{{a^2}}}{c}} \right)} \right| = \left| {x + \frac{{{a^2}}}{c}} \right|\); \(d(M,{\Delta _2}) = \left| {x - \frac{{{a^2}}}{c}} \right|\)
\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \left| {\frac{{{a^2} + cx}}{a}} \right|:\left| {\frac{{{a^2} + cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\) ;
\(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \left| {\frac{{{a^2} - cx}}{a}} \right|:\left| {\frac{{{a^2} - cx}}{c}} \right| = \left| {\frac{c}{a}} \right| = \frac{c}{a}\)
Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)
Trong mặt phẳng tọa độ Oxy, hypebol (H) có phương trình chính tắc, có tâm sai \(e = 2\) và một đường chuẩn là \(x = 8\). Lập phương trình chính tắc của (H).
Phương pháp giải:
Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
\(c = \sqrt {{a^2} + {b^2}} \)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
+ Đường chuẩn: \({\Delta _1}:x = - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).
Lời giải chi tiết:
Phương trình chính tắc của hypebol có dạng: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
Vì \(a,c > 0\) nên \(e > 0\)
+ Đường chuẩn: \({\Delta _2}:x = 8 = \frac{a}{2} \Rightarrow a = 16\)
+ Tâm sai của hypebol: \(e = 2 \Rightarrow \frac{c}{{16}} = 2 \Rightarrow c = 32 \Rightarrow b = 16\sqrt 3 \)
Phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{256}} - \frac{{{y^2}}}{{768}} = 1\).
Một sao chổi đi qua hệ Mặt Trời theo quỹ đạo là một nhánh hypebol nhận tâm Mặt trời là một tiêu điểm, khoảng cách gần nhất từ sao chổi này đến tâm Mặt trời là \({3.10^8}\) km và tâm sai của quỹ đạo hypebol là 3,6 (H.3.15). Hãy lập phương trình chính tắc của hypebol chứa quỹ đạo, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^8}\) km trên thực tế.
Phương pháp giải:
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_2}(c;0)\) là một tiêu điểm.
Điểm M bất kì thuộc hypebol, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 1\) khi M trùng đỉnh \({A_2}(a;0)\)
+ Tâm sai của hypebol: \(e = \frac{c}{a}\)
Lời giải chi tiết:
\({3.10^8}\) km = 3 đơn vị.
Gọi PTCT của quỹ đạo hình hypebol đó là: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\),
Giả sử Mặt trời là tiêu điểm \({F_2}( - c;0)\).
Điểm M bất kì thuộc hypebol là vị trí của sao chổi trong quỹ đạo, khi đó:
\(M{F_2}\) nhỏ nhất bằng \(c - a = 3\) khi M trùng đỉnh \({A_2}(a;0)\)
Tâm sai của hypebol là: \(e = \frac{c}{a} = 3,6 \Rightarrow c = 3,6a\)
\( \Rightarrow 2,6a = 3 \Leftrightarrow a = \frac{{15}}{{13}},\;c = \frac{{54}}{{13}} \Rightarrow {b^2} = \frac{{207}}{{13}}\)
\( \Rightarrow \)PTCT của hypebol là: \(\frac{{169{x^2}}}{{225}} - \frac{{13{y^2}}}{{207}} = 1\),
Mục 2 của Chuyên đề học tập Toán 10 - Kết nối tri thức tập trung vào việc nghiên cứu về vectơ và các phép toán vectơ. Đây là một phần kiến thức nền tảng quan trọng, không chỉ cho chương trình Toán 10 mà còn là bước đệm cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm và kỹ năng liên quan đến vectơ sẽ giúp học sinh giải quyết các bài toán hình học và vật lý một cách hiệu quả hơn.
Các bài tập trên trang 49 chủ yếu xoay quanh việc hiểu và vận dụng khái niệm vectơ, bao gồm:
Để giải các bài tập này, học sinh cần nắm vững định nghĩa vectơ, các yếu tố của vectơ (điểm đầu, điểm cuối, độ dài, hướng) và cách biểu diễn vectơ trên mặt phẳng tọa độ.
Trang 50 tập trung vào các bài tập về phép cộng và trừ vectơ. Các bài tập này yêu cầu học sinh:
Khi giải các bài tập này, học sinh cần nhớ các quy tắc cộng, trừ vectơ và áp dụng chúng một cách chính xác.
Các bài tập trên trang 51 liên quan đến tích của một số với vectơ. Học sinh cần:
Lưu ý rằng, khi một số âm nhân với một vectơ, vectơ kết quả sẽ ngược hướng với vectơ ban đầu.
Trang 52 là phần tổng hợp các bài tập về vectơ, bao gồm cả các bài tập về khái niệm, phép cộng, trừ vectơ và tích của một số với vectơ. Các bài tập này thường có tính ứng dụng cao, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Bài tập: Cho hai vectơ a = (2; -1) và b = (-3; 4). Tính 2a - b.
Giải:
2a = (4; -2)
2a - b = (4; -2) - (-3; 4) = (4 + 3; -2 - 4) = (7; -6)
Hy vọng với bài giải chi tiết và các phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán về vectơ trong chương trình Toán 10 - Kết nối tri thức. Chúc các em học tốt!