Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 40, 41 của Chuyên đề học tập Toán 10 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Do đó, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải đầy đủ, kèm theo các bước giải thích rõ ràng, giúp học sinh dễ dàng tiếp thu kiến thức và rèn luyện kỹ năng giải toán.
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (H.3.1)
Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.
Phương pháp giải:
Phương trình chính tắc của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
+ Độ dài trục lớn: \(2a\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \)
Lời giải chi tiết:
Ta có:
+ Độ dài trục lớn: \(2a = 10 \Rightarrow a = 5\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} = 6 \Rightarrow \sqrt {{5^2} - {b^2}} = 3 \Rightarrow {b^2} = 16\)
Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
(Phép co đường tròn) Cho đường tròn có phương trình \({x^2} + {y^2} = {a^2}\) và số k \((0 < k < 1)\). Với mỗi điểm \(M({x_0};{y_0})\) thuộc đường tròn, gọi \(H({x_0};0)\) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho \(HN = kHM\) (H.3.5)
a) Tính tọa độ của N theo \({x_0};{y_0};k.\)
b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
Lời giải chi tiết:
Gọi \(N({x_N};{y_N})\).
N thuộc đoạn MH và \(HN = kHM \Rightarrow \overrightarrow {HN} = k\overrightarrow {HM} \)
\(\begin{array}{l} \Leftrightarrow ({x_N} - {x_0};{y_N}) = k(0;{y_0})\\ \Leftrightarrow \left\{ \begin{array}{l}{x_N} - {x_0} = k.0\\{y_N} = k.{y_0}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = {x_0}\\{y_N} = k.{y_0}\end{array} \right.\end{array}\)
Vì \(M({x_0};{y_0})\) thuộc (C) \({x^2} + {y^2} = {a^2}\) nên
\({x_0}^2 + {y_0}^2 = {a^2} \Leftrightarrow {x_N}^2 + {\left( {\frac{{{y_N}}}{k}} \right)^2} = {a^2} \Leftrightarrow \frac{{{x_N}^2}}{{{a^2}}} + \frac{{{y_N}^2}}{{{{(ka)}^2}}} = 1\)
Vậy N thuộc Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (H.3.1)
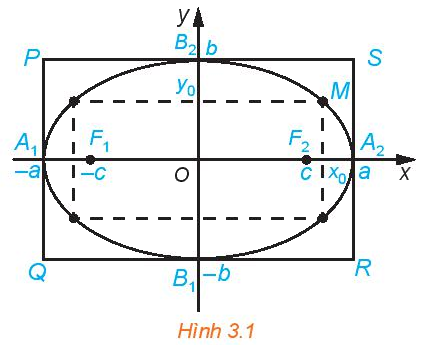
a) Tìm tọa độ các giao điểm của elip với các trục tọa độ
b) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Với điểm \(M({x_0};{y_0})\) thuộc elip, hãy so sánh \(O{M^2}\) với \({a^2},{b^2}\)
Lời giải chi tiết:
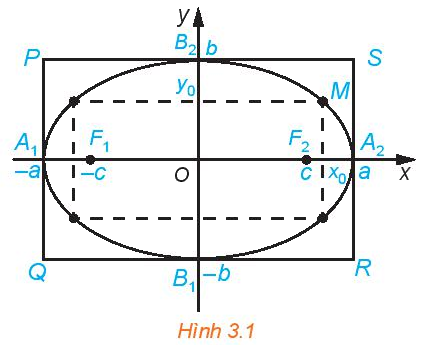
a)
\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)
Giao điểm của elip với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\)
\(x = 0 \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow y = \pm b\)
Giao điểm của elip với Oy là \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
b) Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Từ H.3.1 dễ thấy \(a > b\)
\(\begin{array}{l} \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le 1 \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow {b^2} \le {x_0}^2 + {y_0}^2 \le {a^2}\\ \Leftrightarrow {b^2} \le O{M^2} \le {a^2}\end{array}\)
Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.
Phương pháp giải:
Phương trình chính tắc của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
+ Độ dài trục lớn: \(2a\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \)
Lời giải chi tiết:
Ta có:
+ Độ dài trục lớn: \(2a = 10 \Rightarrow a = 5\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} = 6 \Rightarrow \sqrt {{5^2} - {b^2}} = 3 \Rightarrow {b^2} = 16\)
Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
(Phép co đường tròn) Cho đường tròn có phương trình \({x^2} + {y^2} = {a^2}\) và số k \((0 < k < 1)\). Với mỗi điểm \(M({x_0};{y_0})\) thuộc đường tròn, gọi \(H({x_0};0)\) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho \(HN = kHM\) (H.3.5)
a) Tính tọa độ của N theo \({x_0};{y_0};k.\)
b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
Lời giải chi tiết:
Gọi \(N({x_N};{y_N})\).
N thuộc đoạn MH và \(HN = kHM \Rightarrow \overrightarrow {HN} = k\overrightarrow {HM} \)
\(\begin{array}{l} \Leftrightarrow ({x_N} - {x_0};{y_N}) = k(0;{y_0})\\ \Leftrightarrow \left\{ \begin{array}{l}{x_N} - {x_0} = k.0\\{y_N} = k.{y_0}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = {x_0}\\{y_N} = k.{y_0}\end{array} \right.\end{array}\)
Vì \(M({x_0};{y_0})\) thuộc (C) \({x^2} + {y^2} = {a^2}\) nên
\({x_0}^2 + {y_0}^2 = {a^2} \Leftrightarrow {x_N}^2 + {\left( {\frac{{{y_N}}}{k}} \right)^2} = {a^2} \Leftrightarrow \frac{{{x_N}^2}}{{{a^2}}} + \frac{{{y_N}^2}}{{{{(ka)}^2}}} = 1\)
Vậy N thuộc Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (H.3.1)
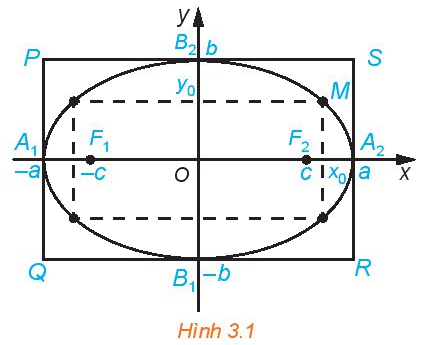
a) Tìm tọa độ các giao điểm của elip với các trục tọa độ
b) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Với điểm \(M({x_0};{y_0})\) thuộc elip, hãy so sánh \(O{M^2}\) với \({a^2},{b^2}\)
Lời giải chi tiết:
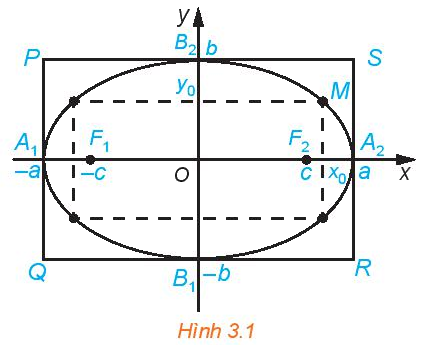
a)
\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)
Giao điểm của elip với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\)
\(x = 0 \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow y = \pm b\)
Giao điểm của elip với Oy là \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
b) Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Từ H.3.1 dễ thấy \(a > b\)
\(\begin{array}{l} \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le 1 \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow {b^2} \le {x_0}^2 + {y_0}^2 \le {a^2}\\ \Leftrightarrow {b^2} \le O{M^2} \le {a^2}\end{array}\)
Mục 1 của Chuyên đề học tập Toán 10 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững các khái niệm cơ bản và áp dụng chúng vào giải quyết các bài toán thực tế. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để đạt được kết quả tốt. Trong mục này, chúng ta sẽ đi sâu vào phân tích từng bài tập trang 40 và 41, cung cấp lời giải chi tiết và các phương pháp tiếp cận hiệu quả.
Bài tập 1 thường là bài tập khởi động, giúp học sinh ôn lại kiến thức đã học và làm quen với dạng bài mới. Để giải bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu tính giá trị của một biểu thức, chúng ta cần thay các giá trị đã cho vào biểu thức và thực hiện các phép tính theo đúng thứ tự ưu tiên. Sau khi tính toán xong, chúng ta cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập 2 thường là bài tập nâng cao, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn. Để giải bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu tìm điều kiện để một phương trình có nghiệm, chúng ta cần phân tích các yếu tố ảnh hưởng đến nghiệm của phương trình và xây dựng các bất đẳng thức tương ứng. Sau đó, chúng ta giải các bất đẳng thức này để tìm ra điều kiện cần và đủ.
Bài tập 3 thường là bài tập tổng hợp, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Để giải bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu giải một hệ phương trình, chúng ta có thể sử dụng phương pháp thế, phương pháp cộng đại số hoặc phương pháp ma trận. Sau khi giải xong, chúng ta cần kiểm tra lại nghiệm để đảm bảo tính chính xác.
Bài tập 4 thường là bài tập ứng dụng, giúp học sinh hiểu rõ hơn về mối liên hệ giữa toán học và thực tế cuộc sống. Để giải bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu tính diện tích của một mảnh đất hình chữ nhật, chúng ta cần đo chiều dài và chiều rộng của mảnh đất, sau đó áp dụng công thức tính diện tích hình chữ nhật.
Để học tập Toán 10 hiệu quả, bạn nên:
Việc giải bài tập Toán 10 - Kết nối tri thức đòi hỏi sự kiên trì, cẩn thận và tư duy logic. Hy vọng rằng với lời giải chi tiết và các phương pháp tiếp cận hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc học tập và đạt được kết quả tốt nhất.