Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 Chuyên đề học tập Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
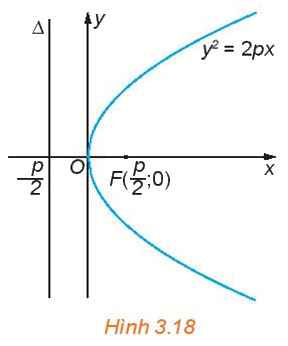
Cho parabol có phương trình chính tắc \(y = 2px\) (H.3.18).
Trongg mặt phẳng tọa độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm A(6;6). Tìm tham số tiêu và phương trình đường chuẩn của (P)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tham số tiêu: p
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
Gọi PTCT của (P) là \({y^2} = 2px\)
Vì \(A\left( {6;6} \right) \in (P)\) nên \({6^2} = 2.p.6 \Rightarrow p = 3\)
+ Tham số tiêu: p = 3
+ Đường chuẩn: \(\Delta :x = - \frac{3}{2}\)
Cho parabol có phương trình chính tắc \(y = 2px\) (H.3.18).
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì điểm \(N({x_0}; - {y_0})\) có thuộc parabol hay không?
b) Từ phương trình chính tắc của parabol, có thể rút ra điều gì về hoành độ của những điểm thuộc parabol?
Lời giải chi tiết:
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)
nên điểm \(N({x_0}; - {y_0})\) có thuộc parabol.
b)
Với p>0 thì các điểm thuộc paranol đều có hoành độ \( \ge 0\).
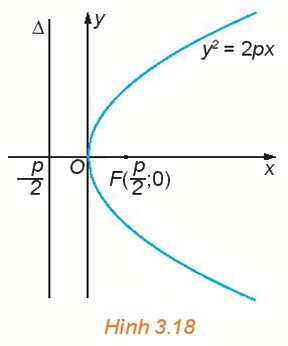
Cho parabol có phương trình chính tắc \(y = 2px\) (H.3.18).
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì điểm \(N({x_0}; - {y_0})\) có thuộc parabol hay không?
b) Từ phương trình chính tắc của parabol, có thể rút ra điều gì về hoành độ của những điểm thuộc parabol?
Lời giải chi tiết:
a) Nếu điểm \(M({x_0};{y_0})\) thuộc parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)
nên điểm \(N({x_0}; - {y_0})\) có thuộc parabol.
b)
Với p>0 thì các điểm thuộc paranol đều có hoành độ \( \ge 0\).
Trongg mặt phẳng tọa độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm A(6;6). Tìm tham số tiêu và phương trình đường chuẩn của (P)
Phương pháp giải:
Cho parabol có PTCT \({y^2} = 2px\)
+ Tham số tiêu: p
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
Gọi PTCT của (P) là \({y^2} = 2px\)
Vì \(A\left( {6;6} \right) \in (P)\) nên \({6^2} = 2.p.6 \Rightarrow p = 3\)
+ Tham số tiêu: p = 3
+ Đường chuẩn: \(\Delta :x = - \frac{3}{2}\)
Mục 1 của Chuyên đề học tập Toán 10 - Kết nối tri thức thường tập trung vào việc ôn tập và mở rộng kiến thức về một chủ đề cụ thể. Trang 54 và 55 thường chứa các bài tập vận dụng, bài tập nâng cao, và các bài toán thực tế liên quan đến kiến thức đã học. Việc giải các bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề.
Để giải quyết hiệu quả các bài tập trong Mục 1, trang 54 và 55, học sinh cần nắm vững các khái niệm, định lý và công thức liên quan. Dưới đây là phân tích chi tiết về các dạng bài tập thường gặp:
Loại bài tập này thường yêu cầu học sinh áp dụng trực tiếp các công thức và định lý đã học để giải quyết các bài toán đơn giản. Ví dụ, tính giá trị của biểu thức, tìm nghiệm của phương trình, hoặc xác định các yếu tố của hình học.
Các bài tập nâng cao thường đòi hỏi học sinh phải suy luận, phân tích và kết hợp nhiều kiến thức khác nhau để tìm ra lời giải. Chúng có thể liên quan đến việc chứng minh các đẳng thức, giải các bài toán phức tạp, hoặc tìm ra các mối liên hệ giữa các khái niệm.
Bài tập thực tế giúp học sinh áp dụng kiến thức Toán học vào các tình huống trong đời sống hàng ngày. Chúng thường liên quan đến việc giải quyết các vấn đề về đo đạc, tính toán, hoặc phân tích dữ liệu.
Để minh họa, chúng ta sẽ cùng giải một số bài tập tiêu biểu trong Mục 1, trang 54 và 55:
Cho phương trình x2 - 5x + 6 = 0. Hãy tìm nghiệm của phương trình.
Lời giải:
Tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Lời giải:
Tọa độ đỉnh của parabol y = ax2 + bx + c là I(-b/2a, -Δ/4a). Trong trường hợp này, a = 1, b = -4, c = 3.
Δ = b2 - 4ac = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4
Vậy, tọa độ đỉnh của parabol là I(2, -1).
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Giải mục 1 trang 54, 55 Chuyên đề học tập Toán 10 - Kết nối tri thức đòi hỏi sự nắm vững kiến thức cơ bản, kỹ năng giải quyết vấn đề và sự kiên trì. Hy vọng rằng với những hướng dẫn và ví dụ trên, bạn sẽ tự tin hơn trong việc giải quyết các bài tập Toán 10 và đạt kết quả tốt nhất.