Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ giải chi tiết các bài tập trong mục 1 của Chuyên đề học tập Toán 10 - Kết nối tri thức, cụ thể là các trang 47, 48, 49 và 50.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc
Cho hyperbol \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\).
a) Tìm tiêu cự và độ dài các trục
b) Tìm các đỉnh và các đường tiệm cận.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
+ Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \)
+ Độ dài trục thực, trục ảo: \(2a,2b\)
+ Hai đỉnh \({A_1}( - a;0),{A_2}(a;0)\)
+ Hai đường tiệm cận \(y = - \frac{b}{a}x\) và \(y = \frac{b}{a}x\)
Lời giải chi tiết:
Ta có hypebol: \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
\( \Rightarrow a = 8,b = 6,c = \sqrt {{a^2} + {b^2}} = 10\)
a) + Tiêu cự: \(2c = 20\)
+ Độ dài trục thực: \(2a = 16\); trục ảo \(2b = 12.\)
b) + Hai đỉnh \({A_1}( - 8;0),{A_2}(8;0)\)
+ Hai đường tiệm cận \(y = - \frac{3}{4}x\) và \(y = \frac{3}{4}x\)
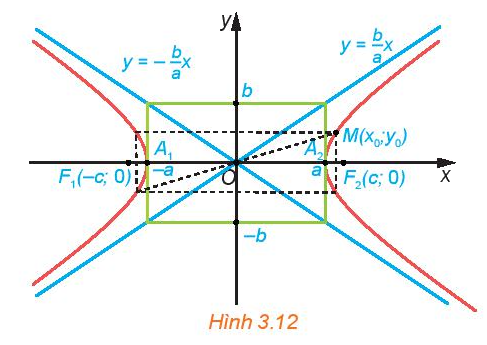
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
a) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc hypebol (H.3.12).
b) Tìm tọa độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm \(M({x_0};{y_0})\) thuộc hypebol, hãy so sánh \(\left| {{x_0}} \right|\) với \(a\)
Lời giải chi tiết:
a) Nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Hypebol.
b)
\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)
Giao điểm của hypebol với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\)
\(x = 0 \Rightarrow - \frac{{{y^2}}}{{{b^2}}} = 1\) Vô lý vì \( - \frac{{{y^2}}}{{{b^2}}} \le 0 < 1\)
Vậy hypebol không có giao điểm với trục tung.
c) \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\(\begin{array}{l} \Rightarrow 1 = \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{a^2}}}\\ \Leftrightarrow {x_0}^2 \ge {a^2}\\ \Leftrightarrow \left| {{x_0}} \right| \ge a\end{array}\)
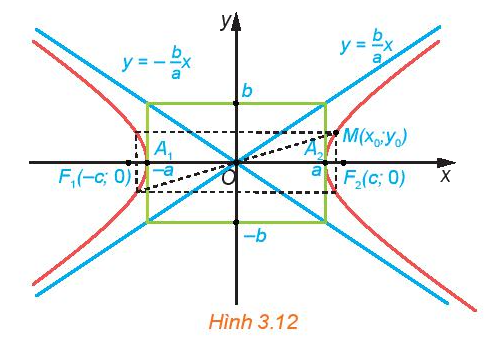
Trong mặt phẳng tọa độ, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\).
a) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc hypebol (H.3.12).
b) Tìm tọa độ các giao điểm của hypebol với trục hoành. Hypebol có cắt trục tung hay không? Vì sao?
c) Với điểm \(M({x_0};{y_0})\) thuộc hypebol, hãy so sánh \(\left| {{x_0}} \right|\) với \(a\)
Lời giải chi tiết:
a) Nếu điểm \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} - \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Hypebol.
b)
\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)
Giao điểm của hypebol với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\)
\(x = 0 \Rightarrow - \frac{{{y^2}}}{{{b^2}}} = 1\) Vô lý vì \( - \frac{{{y^2}}}{{{b^2}}} \le 0 < 1\)
Vậy hypebol không có giao điểm với trục tung.
c) \(M({x_0};{y_0})\) thuộc hypebol thì \(\frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\(\begin{array}{l} \Rightarrow 1 = \frac{{{x_0}^2}}{{{a^2}}} - \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{a^2}}}\\ \Leftrightarrow {x_0}^2 \ge {a^2}\\ \Leftrightarrow \left| {{x_0}} \right| \ge a\end{array}\)
Cho hyperbol \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\).
a) Tìm tiêu cự và độ dài các trục
b) Tìm các đỉnh và các đường tiệm cận.
Phương pháp giải:
Phương trình của hypebol \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
+ Tiêu cự: \(2c = 2\sqrt {{a^2} + {b^2}} \)
+ Độ dài trục thực, trục ảo: \(2a,2b\)
+ Hai đỉnh \({A_1}( - a;0),{A_2}(a;0)\)
+ Hai đường tiệm cận \(y = - \frac{b}{a}x\) và \(y = \frac{b}{a}x\)
Lời giải chi tiết:
Ta có hypebol: \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
\( \Rightarrow a = 8,b = 6,c = \sqrt {{a^2} + {b^2}} = 10\)
a) + Tiêu cự: \(2c = 20\)
+ Độ dài trục thực: \(2a = 16\); trục ảo \(2b = 12.\)
b) + Hai đỉnh \({A_1}( - 8;0),{A_2}(8;0)\)
+ Hai đường tiệm cận \(y = - \frac{3}{4}x\) và \(y = \frac{3}{4}x\)
Mục 1 của Chuyên đề học tập Toán 10 - Kết nối tri thức thường tập trung vào các khái niệm cơ bản về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các phần tiếp theo của chương trình.
Các bài tập trên trang 47 thường xoay quanh việc xác định vectơ, biểu diễn vectơ, và so sánh các vectơ. Để giải các bài tập này, học sinh cần nắm vững định nghĩa vectơ, các ký hiệu vectơ, và các tính chất cơ bản của vectơ.
Trang 48 tập trung vào các bài tập về phép cộng và phép trừ vectơ. Học sinh cần nắm vững quy tắc cộng và trừ vectơ, cũng như các tính chất của phép cộng và phép trừ vectơ.
Các bài tập trên trang 49 liên quan đến tích của một số với vectơ. Học sinh cần hiểu rõ ý nghĩa của tích của một số với vectơ, cũng như quy tắc tính tích của một số với vectơ.
Ví dụ: Cho vectơ a = (x; y) và số thực k. Tích của k với vectơ a là vectơ ka = (kx; ky).
Trang 50 thường chứa các bài tập tổng hợp, kết hợp các kiến thức đã học trong mục 1. Các bài tập này có thể yêu cầu học sinh áp dụng kiến thức về vectơ để giải quyết các bài toán hình học.
| Bài tập | Nội dung |
|---|---|
| Bài 6 | Chứng minh rằng bốn điểm A, B, C, D là các đỉnh của một hình bình hành. |
| Bài 7 | Tìm tọa độ của điểm M sao cho vectơ AM bằng vectơ BC. |
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với bộ giải chi tiết này, các em học sinh sẽ tự tin hơn trong việc học tập và giải bài tập Toán 10. Chúc các em học tốt!