Bài học Toán lớp 5 Bài 43: Hình tam giác thuộc chương trình SGK Chân trời sáng tạo giúp các em học sinh nắm vững kiến thức về hình tam giác, các yếu tố của hình tam giác và cách tính diện tích hình tam giác.
Tại giaitoan.edu.vn, các em sẽ được cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách giáo khoa, cùng với các bài tập vận dụng để củng cố kiến thức.
Đề bài Nêu tên các hình tam giác, các cạnh, các góc của mỗi hình tam giác dưới đây và cho biết tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù. tam giác đều. Nêu đường cao và đáy tương ứng được vẽ trong mỗi hình tam giác dưới đây. Dùng ê-ke, thước thẳng để vẽ đường cao tương ứng với đáy BC của tam giác ABC và đáy PR của tam giác PQR (sử dụng tờ giấy có hình vẽ các tam giác như hình bên).
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 90 SGK Toán 5 Chân trời sáng tạo
Nêu đường cao và đáy tương ứng được vẽ trong mỗi hình tam giác dưới đây. 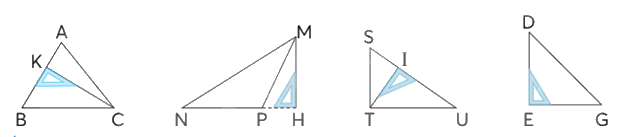
Phương pháp giải:
Dựa vào lý thuyết về đáy và đường cao trong tam giác.
Lời giải chi tiết:
- Hình tam giác ABC: Đáy là AB, đường cao tương ứng là CK.
- Hình tam giác MNP: Đáy là NP, đường cao tương ứng là MH.
- Hình tam giác STU: Đáy là SU, đường cao tương ứng là TI.
- Hình tam giác DEG: Đáy là EG, đường cao tương ứng là DE.
Video hướng dẫn giải
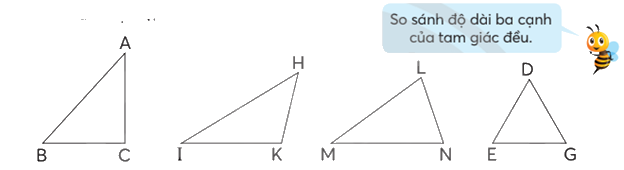
Nêu tên các hình tam giác, các cạnh, các góc của mỗi hình tam giác dưới đây và cho biết tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù. tam giác đều.
Phương pháp giải:
Dựa vào tính chất của các tam giác:
- Hình tam giác có một góc vuông là tam giác vuông.
- Hình tam giác có một góc tù là tam giác tù.
- Hình tam giác có ba góc nhọn là tam giác nhọn.
- Hình tam giác có ba góc 600 là tam giác đều.
Lời giải chi tiết:
- Hình tam giác ABC là tam giác vuông có: các cạnh AB, BC, AC và các góc đỉnh A, góc đỉnh B, góc vuông đỉnh C.
- Hình tam giác HKI là tam giác tù có: các cạnh HK, KI, HI và các góc đỉnh H, góc đỉnh I, góc tù đỉnh K.
- Hình tam giác LMN là tam giác nhọn có: các cạnh LN, LM, MN và các góc đỉnh L, góc đỉnh M, góc đỉnh N.
- Hình tam giác DEG là tam giác đều có: các cạnh DE, EG, DG và các góc đỉnh D, góc đỉnh E, góc đỉnh G.
Ta có: độ dài các cạnh của tam giác đều bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Khám phá trang 90 SGK Toán 5 Chân trời sáng tạo
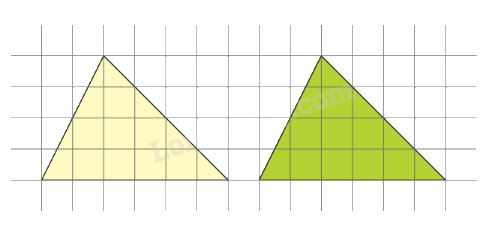
An đố Nhiên: Mình có hai tấm bìa hình tam giác như hình bên. Làm thế nào để cắt một hình thành hai mảnh rồi ghép với hình còn lại để được một hình chữ nhật? Em hãy giúp bạn Nhiên nhé!
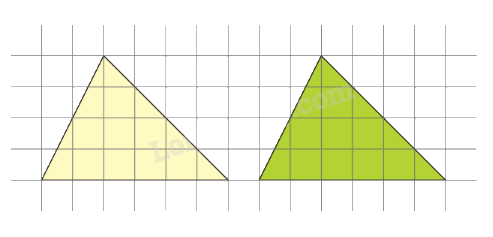
Phương pháp giải:
Vận dụng tính chất về đường cao của tam giác, tính chất của hình chữ nhật.
Lời giải chi tiết:
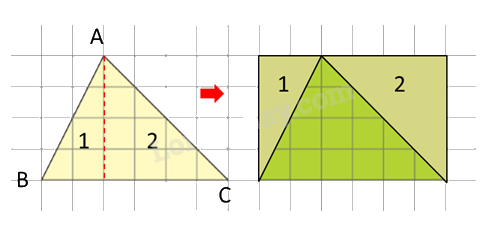
Vì 2 hình tam giác có kích thước bằng nhau nên ta cắt hình tam giác nhạt màu thành 2 hình tam giác bé theo đường cao tương ứng với đáy BC.
Sau đó ghép lại ta được hình chữ nhật từ hai hình tam giác đã cho.
Video hướng dẫn giải
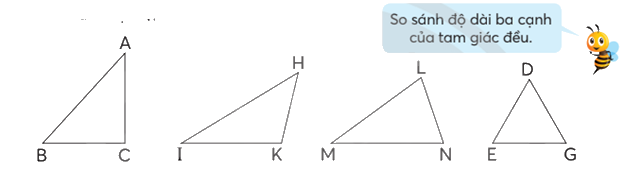
Nêu tên các hình tam giác, các cạnh, các góc của mỗi hình tam giác dưới đây và cho biết tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù. tam giác đều.
Phương pháp giải:
Dựa vào tính chất của các tam giác:
- Hình tam giác có một góc vuông là tam giác vuông.
- Hình tam giác có một góc tù là tam giác tù.
- Hình tam giác có ba góc nhọn là tam giác nhọn.
- Hình tam giác có ba góc 600 là tam giác đều.
Lời giải chi tiết:
- Hình tam giác ABC là tam giác vuông có: các cạnh AB, BC, AC và các góc đỉnh A, góc đỉnh B, góc vuông đỉnh C.
- Hình tam giác HKI là tam giác tù có: các cạnh HK, KI, HI và các góc đỉnh H, góc đỉnh I, góc tù đỉnh K.
- Hình tam giác LMN là tam giác nhọn có: các cạnh LN, LM, MN và các góc đỉnh L, góc đỉnh M, góc đỉnh N.
- Hình tam giác DEG là tam giác đều có: các cạnh DE, EG, DG và các góc đỉnh D, góc đỉnh E, góc đỉnh G.
Ta có: độ dài các cạnh của tam giác đều bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 90 SGK Toán 5 Chân trời sáng tạo
Nêu đường cao và đáy tương ứng được vẽ trong mỗi hình tam giác dưới đây. 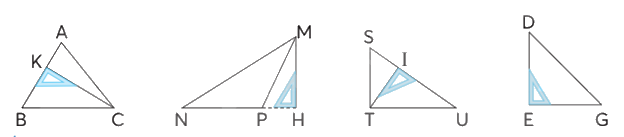
Phương pháp giải:
Dựa vào lý thuyết về đáy và đường cao trong tam giác.
Lời giải chi tiết:
- Hình tam giác ABC: Đáy là AB, đường cao tương ứng là CK.
- Hình tam giác MNP: Đáy là NP, đường cao tương ứng là MH.
- Hình tam giác STU: Đáy là SU, đường cao tương ứng là TI.
- Hình tam giác DEG: Đáy là EG, đường cao tương ứng là DE.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 90 SGK Toán 5 Chân trời sáng tạo
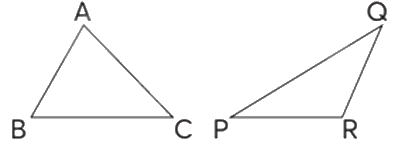
Dùng ê-ke, thước thẳng để vẽ đường cao tương ứng với đáy BC của tam giác ABC và đáy PR của tam giác PQR (sử dụng tờ giấy có hình vẽ các tam giác như hình bên).
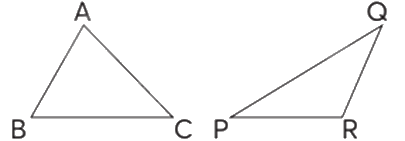
Phương pháp giải:
- Cách vẽ đường cao tương ứng với đáy BC của tam giác ABC:
Bước 1: Đặt ê-ke.
Bước 2: Vẽ
Bước 3: Ghi tên đường cao.
- Cách vẽ đường cao tương ứng với đáy PR của tam giác PQR:
Bước 1: Vẽ kéo dài cạnh PR.
Bước 2: Đặt ê-ke và Vẽ
Bước 3: Ghi tên đường cao.
Lời giải chi tiết:
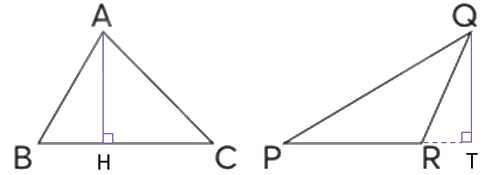
Video hướng dẫn giải
Trả lời câu hỏi Khám phá trang 90 SGK Toán 5 Chân trời sáng tạo
An đố Nhiên: Mình có hai tấm bìa hình tam giác như hình bên. Làm thế nào để cắt một hình thành hai mảnh rồi ghép với hình còn lại để được một hình chữ nhật? Em hãy giúp bạn Nhiên nhé!
Phương pháp giải:
Vận dụng tính chất về đường cao của tam giác, tính chất của hình chữ nhật.
Lời giải chi tiết:
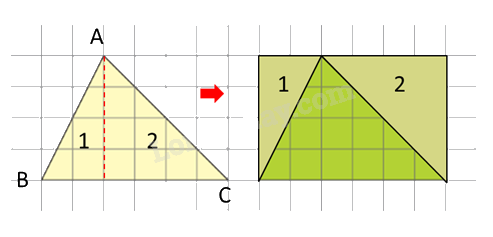
Vì 2 hình tam giác có kích thước bằng nhau nên ta cắt hình tam giác nhạt màu thành 2 hình tam giác bé theo đường cao tương ứng với đáy BC.
Sau đó ghép lại ta được hình chữ nhật từ hai hình tam giác đã cho.
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 90 SGK Toán 5 Chân trời sáng tạo
Dùng ê-ke, thước thẳng để vẽ đường cao tương ứng với đáy BC của tam giác ABC và đáy PR của tam giác PQR (sử dụng tờ giấy có hình vẽ các tam giác như hình bên).
Phương pháp giải:
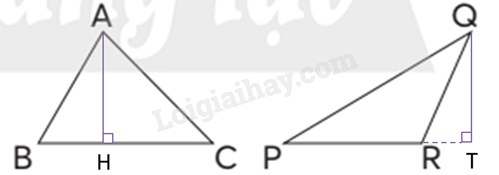
- Cách vẽ đường cao tương ứng với đáy BC của tam giác ABC:
Bước 1: Đặt ê-ke.
Bước 2: Vẽ
Bước 3: Ghi tên đường cao.
- Cách vẽ đường cao tương ứng với đáy PR của tam giác PQR:
Bước 1: Vẽ kéo dài cạnh PR.
Bước 2: Đặt ê-ke và Vẽ
Bước 3: Ghi tên đường cao.
Lời giải chi tiết:
Bài 43 Toán lớp 5 Chân trời sáng tạo giới thiệu về hình tam giác, một trong những hình học cơ bản và quan trọng nhất. Bài học này tập trung vào việc giúp học sinh hiểu rõ khái niệm hình tam giác, các loại tam giác, các yếu tố của tam giác (đỉnh, cạnh, góc) và đặc biệt là cách tính diện tích hình tam giác.
Hình tam giác là hình có ba cạnh và ba góc. Ba cạnh của hình tam giác tạo thành một đa giác khép kín. Các điểm nối giữa hai cạnh gọi là đỉnh của tam giác, và các góc tạo bởi hai cạnh tại đỉnh gọi là góc của tam giác.
Có nhiều cách để phân loại tam giác dựa trên độ dài các cạnh và số đo các góc:
Các yếu tố quan trọng của hình tam giác bao gồm:
Diện tích hình tam giác được tính bằng công thức:
Diện tích = (Đáy x Chiều cao) / 2
Trong đó:
Bài 1: Một tam giác có đáy là 10cm và chiều cao là 8cm. Tính diện tích của tam giác đó.
Giải: Diện tích tam giác là (10cm x 8cm) / 2 = 40cm2
Bài 2: Một tam giác vuông có hai cạnh góc vuông lần lượt là 5cm và 12cm. Tính diện tích của tam giác đó.
Giải: Diện tích tam giác là (5cm x 12cm) / 2 = 30cm2
Khi tính diện tích hình tam giác, cần đảm bảo rằng đơn vị đo đáy và chiều cao phải giống nhau. Nếu không, cần đổi đơn vị trước khi thực hiện phép tính.
Ngoài cách tính diện tích bằng công thức cơ bản, còn có một số công thức khác để tính diện tích tam giác trong các trường hợp đặc biệt, chẳng hạn như công thức Heron khi biết độ dài ba cạnh của tam giác.
Hy vọng bài học Toán lớp 5 Bài 43: Hình tam giác - SGK Chân trời sáng tạo này sẽ giúp các em học sinh hiểu rõ hơn về hình tam giác và cách tính diện tích của nó. Chúc các em học tốt!