Bài 26 thuộc chương trình Toán 2 Kết nối tri thức với cuộc sống, tập trung vào việc ôn luyện kiến thức về đường gấp khúc và làm quen với hình tứ giác. Bài học này giúp các em học sinh rèn luyện kỹ năng nhận biết, phân loại và vẽ các hình dạng cơ bản.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Vở bài tập Toán 2, giúp các em học sinh tự tin hơn trong quá trình học tập.
Khoanh vào vật có dạng đường gấp khúc và dạng hình tứ giác trong bức tranh bên dưới. Vẽ một đường kẻ chia hình dưới đây thành hai phần: một phần chỉ có hình tứ giác, một phần chỉ có hình tam giác. Hai bạn ốc sên Bu và Bi bò qua sân theo hai đường như hình vẽ.
Cho hình vẽ:
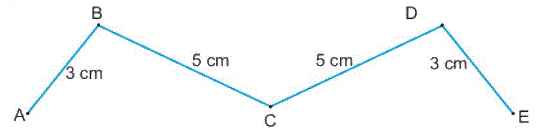
a) Viết tên các đường gấp khúc thích hợp vào chỗ chấm.
Các đường gấp khúc gồm 3 đoạn thẳng là:............................................................................
Đường gấp khúc gồm 4 đoạn thẳng là:..................................................................................
b) Tính độ dài đường gấp khúc BCDE.
Phương pháp giải:
- Quan sát hình vẽ rồi viết tên các đường gấp khúc gồm 3 đoạn thẳng, 4 đoạn thẳng.
- Độ dài đường gấp khúc BCDE là tổng độ dài các đoạn thẳng BC, CD, DE.
Lời giải chi tiết:
a) Các đường gấp khúc gồm 3 đoạn thẳng là: ABCD, BCDE.
Đường gấp khúc gồm 4 đoạn thẳng là: ABCDE.
b) Độ dài đường gấp khúc BCDE là
5 + 5 + 3 = 13 (cm)
Đáp số: 13 cm
Hai bạn ốc sên Bu và Bi bò qua sân theo hai đường như hình vẽ.

Viết tiếp vào chỗ chấm cho thích hợp.
a) Bu bò quãng đường dài ..... cm. Bi bò quãng đường dài ....... cm.
b) Bạn ......... bò quãng đường dài hơn.
Phương pháp giải:
Quan sát hình vẽ, tính độ dài quãng đường mỗi bạn bò được rồi điền vào chỗ chấm.
Lời giải chi tiết:
a) Bu bò quãng đường dài 10 cm. Bi bò quãng đường dài 11 cm.
b) Bạn Bi bò quãng đường dài hơn.
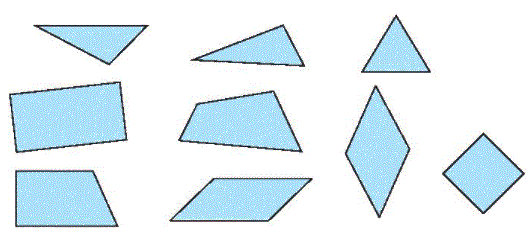
Vẽ một đường kẻ chia hình dưới đây thành hai phần: một phần chỉ có hình tứ giác, một phần chỉ có hình tam giác.
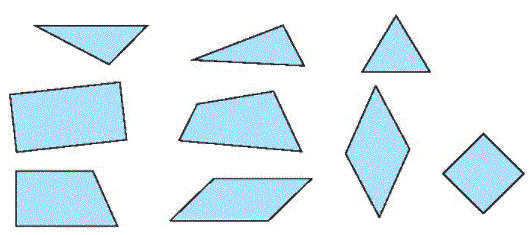
Phương pháp giải:
Quan sát và nhận dạng các hình vẽ rồi kẻ một đường chia hình thành hai phần: một phần chỉ có hình tứ giác, một phần chỉ có hình tam giác.
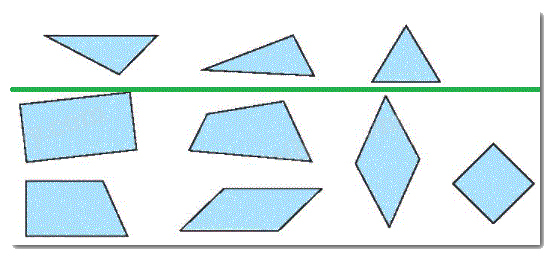
Lời giải chi tiết:
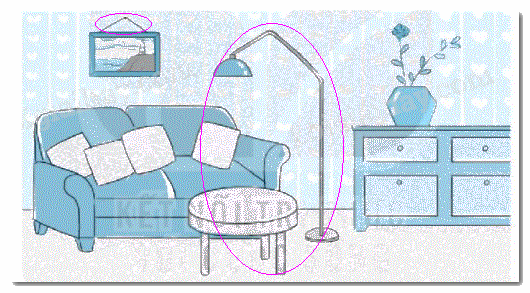
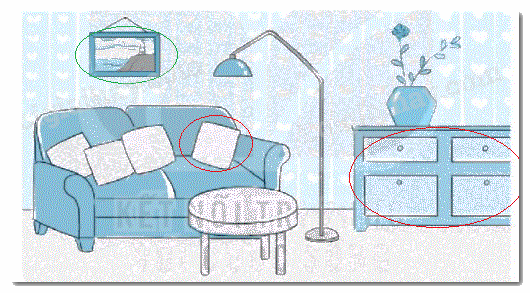
Khoanh vào vật có dạng đường gấp khúc và dạng hình tứ giác trong bức tranh bên dưới.
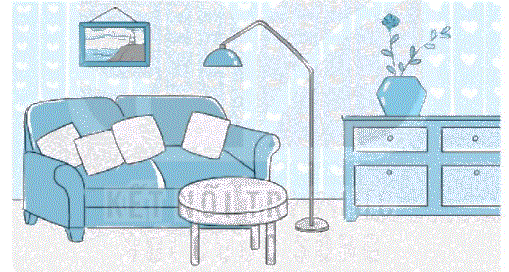
Phương pháp giải:
Quan sát hình vẽ và dựa vào hình dạng của hình tứ giác, đường gấp khúc rồi khoanh vào các vật theo yêu cầu của bài toán.
Lời giải chi tiết:
Các vật có dạng đường gấp khúc:
Các vật có dạng hình tứ giác:
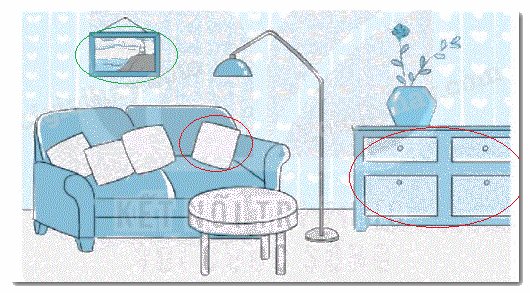
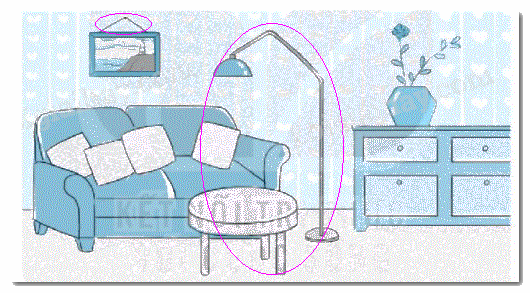
Khoanh vào vật có dạng đường gấp khúc và dạng hình tứ giác trong bức tranh bên dưới.
Phương pháp giải:
Quan sát hình vẽ và dựa vào hình dạng của hình tứ giác, đường gấp khúc rồi khoanh vào các vật theo yêu cầu của bài toán.
Lời giải chi tiết:
Các vật có dạng đường gấp khúc:
Các vật có dạng hình tứ giác:
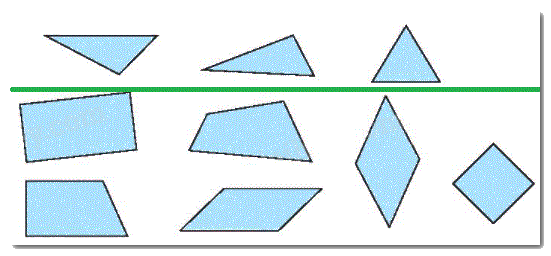
Vẽ một đường kẻ chia hình dưới đây thành hai phần: một phần chỉ có hình tứ giác, một phần chỉ có hình tam giác.
Phương pháp giải:
Quan sát và nhận dạng các hình vẽ rồi kẻ một đường chia hình thành hai phần: một phần chỉ có hình tứ giác, một phần chỉ có hình tam giác.
Lời giải chi tiết:
Cho hình vẽ:
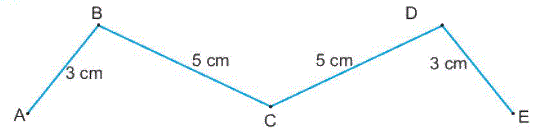
a) Viết tên các đường gấp khúc thích hợp vào chỗ chấm.
Các đường gấp khúc gồm 3 đoạn thẳng là:............................................................................
Đường gấp khúc gồm 4 đoạn thẳng là:..................................................................................
b) Tính độ dài đường gấp khúc BCDE.
Phương pháp giải:
- Quan sát hình vẽ rồi viết tên các đường gấp khúc gồm 3 đoạn thẳng, 4 đoạn thẳng.
- Độ dài đường gấp khúc BCDE là tổng độ dài các đoạn thẳng BC, CD, DE.
Lời giải chi tiết:
a) Các đường gấp khúc gồm 3 đoạn thẳng là: ABCD, BCDE.
Đường gấp khúc gồm 4 đoạn thẳng là: ABCDE.
b) Độ dài đường gấp khúc BCDE là
5 + 5 + 3 = 13 (cm)
Đáp số: 13 cm
Hai bạn ốc sên Bu và Bi bò qua sân theo hai đường như hình vẽ.

Viết tiếp vào chỗ chấm cho thích hợp.
a) Bu bò quãng đường dài ..... cm. Bi bò quãng đường dài ....... cm.
b) Bạn ......... bò quãng đường dài hơn.
Phương pháp giải:
Quan sát hình vẽ, tính độ dài quãng đường mỗi bạn bò được rồi điền vào chỗ chấm.
Lời giải chi tiết:
a) Bu bò quãng đường dài 10 cm. Bi bò quãng đường dài 11 cm.
b) Bạn Bi bò quãng đường dài hơn.
Bài 26 trong Vở bài tập Toán 2 Kết nối tri thức với cuộc sống là một bài học quan trọng giúp củng cố kiến thức về đường gấp khúc và giới thiệu về hình tứ giác. Bài học này không chỉ giúp học sinh hiểu rõ hơn về các khái niệm hình học cơ bản mà còn phát triển khả năng tư duy logic và giải quyết vấn đề.
Thông qua bài học này, học sinh sẽ:
Bài 26 bao gồm các nội dung chính sau:
Bài 1:
Để vẽ một đường gấp khúc gồm 4 đoạn thẳng, em có thể sử dụng thước kẻ và bút chì. Sau khi vẽ xong, em hãy sử dụng thước đo để đo độ dài của từng đoạn thẳng. Cuối cùng, em cộng độ dài của tất cả các đoạn thẳng lại để tìm tổng độ dài của đường gấp khúc.
Ví dụ:
| Đoạn thẳng | Độ dài (cm) |
|---|---|
| Đoạn 1 | 5 |
| Đoạn 2 | 3 |
| Đoạn 3 | 4 |
| Đoạn 4 | 2 |
Tổng độ dài đường gấp khúc: 5 + 3 + 4 + 2 = 14 cm
Bài 2:
Hình tứ giác là hình có bốn cạnh và bốn góc. Khi quan sát các hình đã cho, em hãy tìm những hình nào thỏa mãn điều kiện này. Ví dụ, hình vuông, hình chữ nhật, hình bình hành, hình thang cân đều là những hình tứ giác.
Bài 3:
Để vẽ một hình tứ giác tùy ý, em có thể vẽ bốn đoạn thẳng nối với nhau để tạo thành một hình có bốn cạnh và bốn góc. Em có thể vẽ hình tứ giác với các cạnh và góc khác nhau tùy theo ý thích của mình.
Bài 4:
Bài toán thực tế thường yêu cầu em áp dụng kiến thức về đường gấp khúc và hình tứ giác để giải quyết các vấn đề trong cuộc sống. Em hãy đọc kỹ đề bài, xác định các thông tin cần thiết và sử dụng các công thức hoặc phương pháp phù hợp để tìm ra đáp án.
Để nắm vững kiến thức về đường gấp khúc và hình tứ giác, em nên luyện tập thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online. Em cũng có thể tìm hiểu thêm về các loại hình tứ giác khác nhau và cách vẽ chúng.
Bài tập luyện tập:
Bài 26: Đường gấp khúc. Hình tứ giác (tiết 2) trang 98 Vở bài tập Toán 2 - Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh làm quen với các khái niệm hình học cơ bản và rèn luyện kỹ năng giải quyết vấn đề. Hy vọng rằng, với sự hướng dẫn chi tiết và các bài tập luyện tập, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.