Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chương trình. Bài tập này thường yêu cầu vận dụng các công thức, định lý và phương pháp giải toán đã được trình bày trong chuyên đề.

giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC

Đề bài

Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.

Phương pháp giải - Xem chi tiết Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều 1

- Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).

- Cần xác định vecto \(\overrightarrow u \).

Lời giải chi tiết

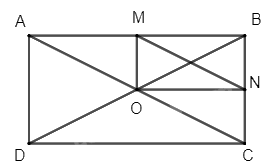
Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều 2

Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC.

Suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \frac{1}{2}\overrightarrow {AC} \,\,(1)\)

Ta có M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và \(MN = \;\frac{1}{2}AC\). Do đó, \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \,\,(2)\)

Từ (1) và (2) suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \overrightarrow {MN} \).

Khi đó, ta có phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến các điểm A, M, O lần lượt thành các điểm O, N, C.

Vậy phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến tam giác AMO thành tam giác ONC.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng toán học. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều: Hướng dẫn chi tiết và đầy đủ

Bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và cách vẽ đồ thị hàm số.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 1 trang 23, học sinh thường được yêu cầu tìm tập xác định, tập giá trị, khoảng đồng biến, khoảng nghịch biến, điểm cực đại, điểm cực tiểu của một hàm số cho trước, hoặc vẽ đồ thị của hàm số đó.

Các bước giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Bước 1: Xác định hàm số: Xác định rõ hàm số được cho trong đề bài.
Bước 2: Tìm tập xác định: Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho hàm số có nghĩa.
Bước 3: Tính đạo hàm: Tính đạo hàm cấp một của hàm số.
Bước 4: Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số.
Bước 5: Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của đạo hàm để xác định khoảng đồng biến và nghịch biến của hàm số.
Bước 6: Tìm cực đại, cực tiểu: Xác định giá trị của hàm số tại các điểm cực trị để tìm cực đại và cực tiểu.
Bước 7: Vẽ đồ thị: Dựa vào các thông tin đã tìm được để vẽ đồ thị của hàm số.

Ví dụ minh họa giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Giả sử hàm số được cho là: y = x³ - 3x² + 2

Tập xác định: R
Đạo hàm: y' = 3x² - 6x
Điểm cực trị: 3x² - 6x = 0 => x = 0 hoặc x = 2
Khoảng đồng biến: (-∞; 0) và (2; +∞)
Khoảng nghịch biến: (0; 2)
Cực đại: Tại x = 0, y = 2
Cực tiểu: Tại x = 2, y = -2

Lưu ý khi giải bài tập

Khi giải bài tập, học sinh cần chú ý các điểm sau:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Nắm vững các khái niệm cơ bản về hàm số và đồ thị.
Sử dụng các công thức và định lý một cách chính xác.
Kiểm tra lại kết quả sau khi giải xong.

Ứng dụng của việc giải bài tập

Việc giải bài tập không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng vận dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.

Tài liệu tham khảo và hỗ trợ học tập

Ngoài sách giáo khoa và sách bài tập, học sinh có thể tham khảo thêm các tài liệu trực tuyến, video bài giảng, và các diễn đàn học tập để nâng cao kiến thức và kỹ năng giải toán. giaitoan.edu.vn là một nguồn tài liệu hữu ích, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 11.

Kết luận

Bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức về hàm số và đồ thị. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các bước giải đúng đắn, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.