Bài 3 trang 43 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
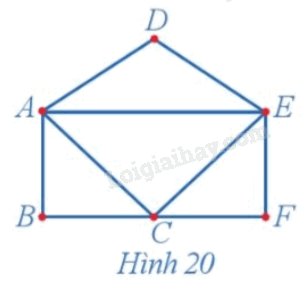
Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Euler (nếu có) của đồ thị ở Hình 20.
Đề bài
Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Euler (nếu có) của đồ thị ở Hình 20.
Phương pháp giải - Xem chi tiết
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần. Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết
Ta có: d(A) = 4, d(B) = 2, d(C) = 4, d(D) = 2, d(E) = 4, d(F) = 2.
Vì đồ thị Hình 20 liên thông và không có đỉnh bậc lẻ nên theo định lí Euler thì đồ thị này có chu trình Euler.
Một chu trình Euler của đồ thị ở Hình 20 là AECFEDACBA.
Bài 3 trang 43 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ứng dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, điểm cực trị, và vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 3 trang 43, học sinh cần xác định hàm số được cho, các điều kiện ràng buộc, và mục tiêu cần đạt được (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất, giải phương trình, hoặc vẽ đồ thị).
Giả sử bài toán yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3].
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Hy vọng hướng dẫn chi tiết này sẽ giúp bạn giải bài 3 trang 43 Chuyên đề học tập Toán 11 Cánh diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!