Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều một cách nhanh chóng và hiệu quả.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận).

Đề bài

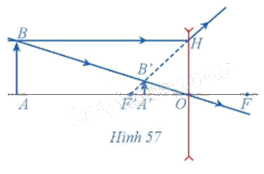
Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận). Vật sáng AB được đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn OA = 60 cm, qua thấu kính cho ảnh ảo A'B' (Hình 57). A'B' là ảnh của AB qua một phép vị tự tâm O tỉ số k.

Tính khoảng cách A'O từ ảnh đến thấu kính và so sánh khoảng cách đó với khoảng cách AO từ vật đến thấu kính.

Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều 2

- Dựa vào định lí Thales

- Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)

Lời giải chi tiết

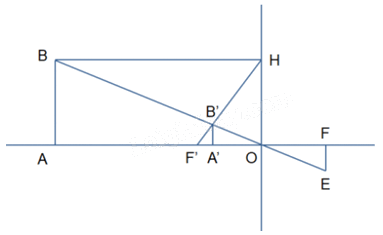
Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều 3

Từ F, kẻ \(EF{\rm{ }}//{\rm{ }}AB{\rm{ }}//{\rm{ }}A'B'\) (F thuộc đường thẳng OB).

Ta có BH = OA = 60 cm.

Vì OF' // BH nên \(\frac{{OB'}}{{BB'}} = \frac{{OF'}}{{BH}} = \frac{{20}}{{60}} = \frac{1}{3}\) (định lí Thales). Suy ra \(OB' = \frac{1}{4}OB\) .

Vì A'B' // AB nên \(\frac{{A'B'}}{{AB}} = \frac{{OB'}}{{OB}} = \frac{1}{4}AB\,\,(1)\)

Vì AB // EF nên \(\frac{{EF}}{{AB}} = \frac{{OF}}{{OA}} = \frac{{20}}{{60}} = \frac{1}{3}\) (định lí Thales). Suy ra \(EF = \frac{1}{3}AB{\rm{ }}\left( 2 \right).\)

Từ (1) và (2) suy ra \(\frac{{A'B'}}{{EF}} = \frac{3}{4}\).

Vì A'B' // EF nên \(\frac{{OA'}}{{OF}} = \frac{{A'B'}}{{EF}} = \frac{3}{4}\) (định lí Thales).

Do đó \(OA' = \frac{3}{4}OF = \frac{3}{4}.20 = 15\,(cm)\).

Ta có: \(\frac{{OA'}}{{OA}} = \frac{{15}}{{60}} = \frac{1}{4}\), suy ra \(OA' = \;\frac{1}{4}OA\).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Ôn tập Toán lớp 11 trên nền tảng toán math. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan

Bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.

Nội dung chi tiết bài 5 trang 33

Bài 5 thường bao gồm các dạng bài tập sau:

Xác định tập xác định của hàm số: Học sinh cần xác định các giá trị của x mà hàm số có nghĩa. Điều này đòi hỏi kiến thức về điều kiện xác định của các phép toán trong hàm số (ví dụ: mẫu số khác 0, căn thức không âm, logarit có cơ số lớn hơn 0 và khác 1).
Tìm tập giá trị của hàm số: Học sinh cần xác định khoảng giá trị mà hàm số có thể nhận được. Điều này có thể được thực hiện bằng cách sử dụng các phương pháp như xét dấu đạo hàm, tìm cực trị hoặc sử dụng kiến thức về các hàm số cơ bản.
Khảo sát sự biến thiên của hàm số: Học sinh cần xác định khoảng đồng biến, khoảng nghịch biến, cực đại, cực tiểu của hàm số. Điều này được thực hiện bằng cách xét dấu đạo hàm bậc nhất.
Vẽ đồ thị hàm số: Học sinh cần vẽ đồ thị hàm số dựa trên các thông tin đã thu thập được từ các bước trên.
Ứng dụng đồ thị hàm số để giải các bài toán: Học sinh cần sử dụng đồ thị hàm số để giải các bài toán liên quan đến việc tìm nghiệm của phương trình, bất phương trình hoặc xác định các giá trị của hàm số tại một điểm cụ thể.

Phương pháp giải bài tập hiệu quả

Để giải bài tập bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, bạn nên:

Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các khái niệm và định lý liên quan đến hàm số, đồ thị hàm số và các phép biến đổi hàm số.
Phân tích đề bài cẩn thận: Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Sử dụng các phương pháp phù hợp: Lựa chọn phương pháp giải phù hợp với từng dạng bài tập cụ thể.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Bài toán: Xét hàm số y = x² - 4x + 3. Hãy xác định tập xác định, tập giá trị, khoảng đồng biến, khoảng nghịch biến và vẽ đồ thị hàm số.

Giải:

Tập xác định: D = ℝ (hàm số xác định với mọi x thuộc tập số thực).
Tập giá trị: y ≥ -1 (hàm số đạt giá trị nhỏ nhất tại x = 2, y = -1).
Khoảng đồng biến: (2, +∞).
Khoảng nghịch biến: (-∞, 2).
Đồ thị hàm số: Đồ thị hàm số là một parabol có đỉnh tại (2, -1) và mở lên trên.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Hãy tìm kiếm các bài giải chi tiết trên giaitoan.edu.vn để hiểu rõ hơn về cách giải các bài tập này.

Kết luận

Bài 5 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải các bài toán liên quan đến hàm số và đồ thị hàm số. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn trong quá trình học tập và giải bài tập.