Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chuyên đề học tập Cánh Diều. Mục 3 trang 40, 41, 42, 43 là một phần quan trọng trong chương trình học, đòi hỏi sự nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải chi tiết, giúp bạn hiểu rõ bản chất của từng bài tập và áp dụng kiến thức vào thực tế.
Quan sát đồ thị ở Hình 10 và đường đi CABDCB, cho biết:
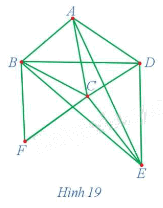
Chứng minh rằng đồ thị G ở Hình 19 có ít nhất một chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
Đồ thị G ở Hình 19 gồm 6 đỉnh, trong đó các đỉnh A, D, E có bậc 4, các đỉnh B, C có bậc 5 và đỉnh F có bậc 2 nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 6. Do đó, theo định lí Ore, đồ thị G có ít nhất một chu trình Hamilton.
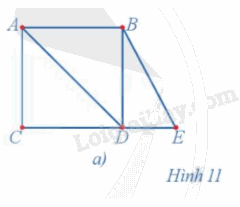
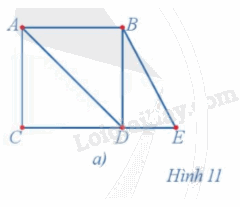
Hãy chỉ ra hai đường đi Euler trong đồ thị ở Hình 11a.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Lời giải chi tiết:
Hình 11a có đường đi Euler BEDBADCA và đường đi Euler BEDCADBA.
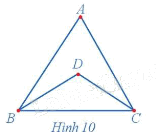
Quan sát đồ thị ở Hình 10 và đường đi CABDCB, cho biết:
a) Đường đi trên có đi qua tất cả các cạnh của đồ thị hay không?
b) Đường đi trên đi qua mỗi cạnh bao nhiêu lần?
Phương pháp giải:
Quan sát hình 10 để trả lời
Lời giải chi tiết:
Quan sát đồ thị ở Hình 10 ta thấy:
a) Đường đi CABDCB đi qua tất cả các cạnh của đồ thị.
b) Đường đi trên đi qua mỗi cạnh đúng một lần.
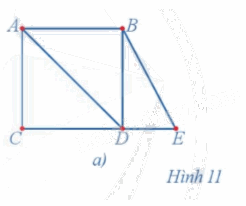
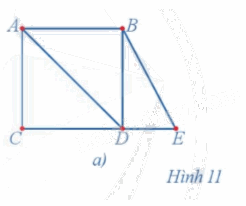
Chứng minh rằng đồ thị ở Hình 11a không có chu trình Euler.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
Ta có d(A) = 3, d(B) = 3 nên đồ thị ở Hình 11a có đỉnh bậc lẻ, do đó theo định lí Euler, đồ thị ở Hình 11a không có chu trình Euler.
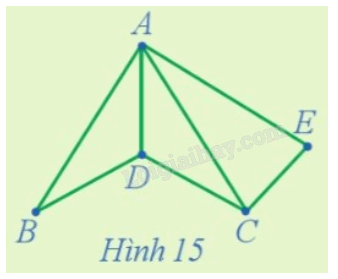
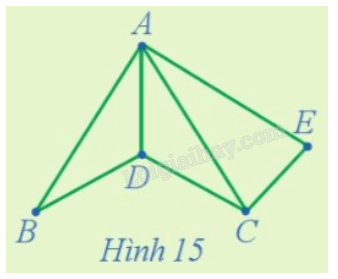
Tìm hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị trong Hình 15.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Lời giải chi tiết:
Quan sát đồ thị Hình 15, ta thấy rằng hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị này là EACDB và ECDBA.
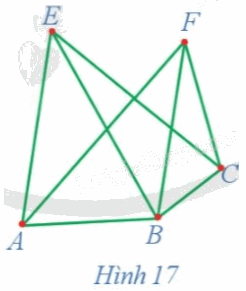
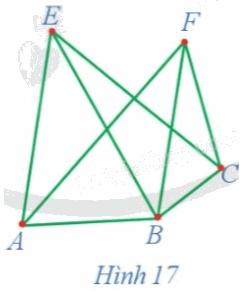
Chứng minh rằng đồ thị G ở Hình 17 có ít nhất một chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton
Lời giải chi tiết:
Ta có: d(A) = 3, d(B) = 4, d(C) = 3, d(E) = 3, d(F) = 3. Đồ thị G ở Hình 17 gồm 5 đỉnh, mỗi đỉnh của đồ thị đều có bậc không nhỏ hơn \(\frac{5}{2}\) . Do đó, theo định lí Dirac, đồ thị G có ít nhất một chu trình Hamilton.
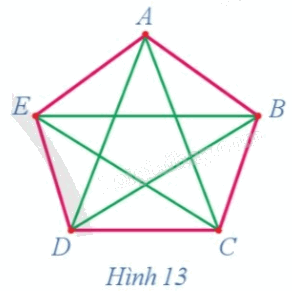
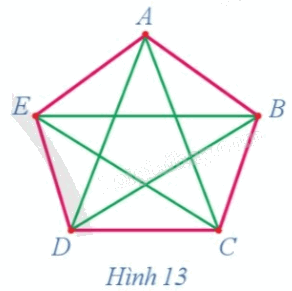
Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 và cho biết đường đi đó có đi qua tất cả các đỉnh của đồ thị hay không và mỗi đỉnh đi qua bao nhiêu lần.
Phương pháp giải:
Quan sát hình 13 để trả lời
Lời giải chi tiết:
Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 ta thấy đường đi đó đi qua tất cả các đỉnh của đồ thị hay và mỗi đỉnh đi qua đúng một lần.
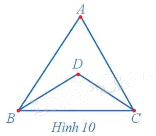
Quan sát đồ thị ở Hình 10 và đường đi CABDCB, cho biết:
a) Đường đi trên có đi qua tất cả các cạnh của đồ thị hay không?
b) Đường đi trên đi qua mỗi cạnh bao nhiêu lần?
Phương pháp giải:
Quan sát hình 10 để trả lời
Lời giải chi tiết:
Quan sát đồ thị ở Hình 10 ta thấy:
a) Đường đi CABDCB đi qua tất cả các cạnh của đồ thị.
b) Đường đi trên đi qua mỗi cạnh đúng một lần.
Hãy chỉ ra hai đường đi Euler trong đồ thị ở Hình 11a.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Lời giải chi tiết:
Hình 11a có đường đi Euler BEDBADCA và đường đi Euler BEDCADBA.
Chứng minh rằng đồ thị ở Hình 11a không có chu trình Euler.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết:
Ta có d(A) = 3, d(B) = 3 nên đồ thị ở Hình 11a có đỉnh bậc lẻ, do đó theo định lí Euler, đồ thị ở Hình 11a không có chu trình Euler.
Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 và cho biết đường đi đó có đi qua tất cả các đỉnh của đồ thị hay không và mỗi đỉnh đi qua bao nhiêu lần.
Phương pháp giải:
Quan sát hình 13 để trả lời
Lời giải chi tiết:
Quan sát đường đi màu đỏ trên đồ thị ở Hình 13 ta thấy đường đi đó đi qua tất cả các đỉnh của đồ thị hay và mỗi đỉnh đi qua đúng một lần.
Tìm hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị trong Hình 15.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Lời giải chi tiết:
Quan sát đồ thị Hình 15, ta thấy rằng hai đường đi Hamilton bắt đầu từ đỉnh E của đồ thị này là EACDB và ECDBA.
Chứng minh rằng đồ thị G ở Hình 17 có ít nhất một chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton
Lời giải chi tiết:
Ta có: d(A) = 3, d(B) = 4, d(C) = 3, d(E) = 3, d(F) = 3. Đồ thị G ở Hình 17 gồm 5 đỉnh, mỗi đỉnh của đồ thị đều có bậc không nhỏ hơn \(\frac{5}{2}\) . Do đó, theo định lí Dirac, đồ thị G có ít nhất một chu trình Hamilton.
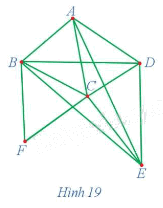
Chứng minh rằng đồ thị G ở Hình 19 có ít nhất một chu trình Hamilton.
Phương pháp giải:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết:
Đồ thị G ở Hình 19 gồm 6 đỉnh, trong đó các đỉnh A, D, E có bậc 4, các đỉnh B, C có bậc 5 và đỉnh F có bậc 2 nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 6. Do đó, theo định lí Ore, đồ thị G có ít nhất một chu trình Hamilton.
Mục 3 trong Chuyên đề học tập Toán 11 Cánh Diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, đây có thể là một chương về hàm số, phương trình, bất phương trình, hoặc các chủ đề hình học không gian. Việc nắm bắt được nội dung chính sẽ giúp bạn định hướng được phương pháp giải bài tập phù hợp.
Có nhiều phương pháp giải bài tập hiệu quả, tùy thuộc vào từng dạng bài cụ thể. Dưới đây là một số phương pháp thường được sử dụng:
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 3 trang 40, 41, 42, 43 Chuyên đề học tập Toán 11 Cánh Diều:
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Đề bài: (Giả định một đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập)
Trong quá trình giải bài tập, bạn cần lưu ý một số điểm sau:
Hy vọng rằng với bộ giải chi tiết này, bạn sẽ tự tin hơn trong việc giải các bài tập Mục 3 trang 40, 41, 42, 43 Chuyên đề học tập Toán 11 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao!