Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 24 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Quan sát Hình 42 và chỉ ra hai phép dời hình (phân biệt) biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
Đề bài
Quan sát Hình 42 và chỉ ra hai phép dời hình (phân biệt) biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
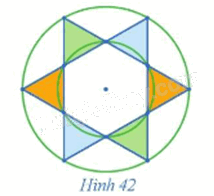
Phương pháp giải - Xem chi tiết
Quan sát hình 42 và sử dụng kiến thức về các phép biến hình đã học để làm
Lời giải chi tiết
+) Đặt các điểm như hình vẽ.
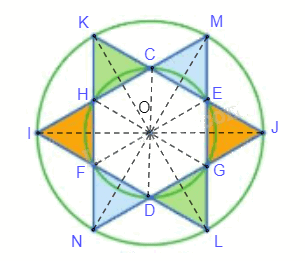
Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, GH nên O là trung điểm của CD, EF, GH. Đường tròn lớn tâm O có các đường kính MN, LK, IJ nên O là trung điểm của MN, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm C, M, E, J, G, L, D tương ứng thành các điểm D, N, F, I, H, K, C.
Từ đó suy ra phép đối xứng tâm O biến các tam giác CME, EJG, GLD, FDN, FHI, KHC tương ứng thành các tam giác DNF, FIH, HKC, ECM, EGJ, LGD hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
+) Đặt các điểm như hình vẽ:
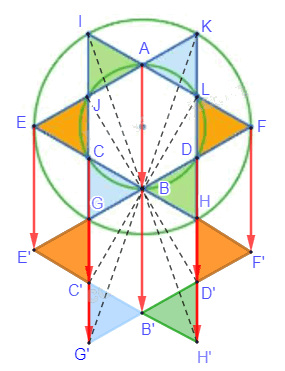
- Phép tịnh tiến theo vectơ \(\overrightarrow {AB} \) biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H'.
- Phép đối xứng tâm B biến các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H' lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI.
Do đó, ta có phép dời hình F có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow {AB} \) và phép đối xứng tâm B ( \({T_{\overrightarrow {AB} }}\) trước, sau) biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI hay chính là phép dời hình F đó biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
Bài 8 trang 24 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 24 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, học sinh cần:
Bài toán: Xét hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, tính đơn điệu và vẽ đồ thị của hàm số.
Giải:
Khi giải bài tập về hàm số, học sinh cần chú ý đến các điều kiện xác định của hàm số và sử dụng các phương pháp biến đổi hàm số một cách linh hoạt. Ngoài ra, việc vẽ đồ thị hàm số giúp học sinh hiểu rõ hơn về tính chất của hàm số và kiểm tra lại kết quả của mình.
Bài 8 trang 24 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và rèn luyện kỹ năng giải toán. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.