Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 24 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu sâu hơn về kiến thức đã học.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các tài liệu học tập chất lượng và lời giải bài tập chính xác.
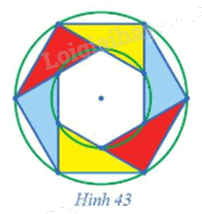
Quan sát Hình 43 và chỉ ra:
Đề bài
Quan sát Hình 43 và chỉ ra:
a) Một phép dời hình biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Một phép dời hình biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay
Lời giải chi tiết
Đặt các điểm như hình vẽ.
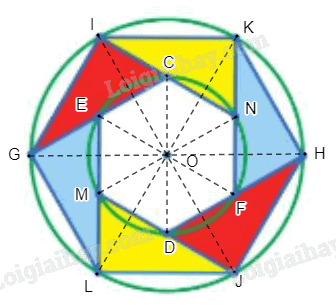
a) Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, MN nên O là trung điểm của CD, EF, MN. Đường tròn lớn tâm O có các đường kính GH, LK, IJ nên O là trung điểm của GH, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm I, K, N, H, F, D, J tương ứng thành các điểm J, L, M, G, E, C, I.
Từ đó suy ra phép đối xứng tâm O biến các tam giác IKN, KHF, HJD tương ứng thành các tam giác JLM, LGE, GIC hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
b) Ta có \(\widehat {KOJ} = \frac{{360^\circ }}{3} = 120^\circ \) và \(OK{\rm{ }} = {\rm{ }}OJ\;\) nên ta có phép quay tâm O với góc quay – 120° biến điểm K thành điểm J.
Ta có \(\widehat {HOL} = 120^\circ \) và \(OH{\rm{ }} = {\rm{ }}OL\) nên ta có phép quay tâm O với góc quay – 120° biến điểm H thành điểm L.
Ta có \(\widehat {FOM} = 120^\circ \) và \(OF{\rm{ }} = {\rm{ }}OM\) nên ta có phép quay tâm O với góc quay – 120° biến điểm F thành điểm M.
Do đó, ta có phép quay tâm O với góc quay – 120° biến tam giác KHF thành tam giác JLM.
Tương tự, ta có phép quay tâm O với góc quay – 120° biến tam giác LGE thành tam giác IKN.
Như vậy, phép quay tâm O với góc quay – 120° biến mỗi tam giác được tô màu xanh thành tam giác được tô màu vàng.
Bài 9 trang 24 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là ứng dụng của vectơ trong việc chứng minh các đẳng thức vectơ và giải các bài toán liên quan đến hình học không gian.
Bài 9 trang 24 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 9 trang 24, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi trong bài 9, trang 24, Chuyên đề học tập Toán 11 Cánh diều. Ví dụ:)
Đề bài: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}
Lời giải:
Ta có: vecd{AC'} = vecd{AB} + vecd{BC'} = vecd{AB} + vecd{AD} + vecd{DC'} = vecd{AB} + vecd{AD} + vecd{AA'}. Vậy, overrightarrow{AB} + vecd{AD} + vecd{AA'} = vecd{AC'}.
Đề bài: ...
Lời giải: ...
Vectơ không chỉ là một khái niệm quan trọng trong Toán học mà còn có nhiều ứng dụng trong các lĩnh vực khác như Vật lý, Kỹ thuật, Khoa học máy tính,... Trong Vật lý, vectơ được sử dụng để biểu diễn các đại lượng vật lý có cả độ lớn và hướng, chẳng hạn như vận tốc, lực, gia tốc,... Trong Kỹ thuật, vectơ được sử dụng để mô tả các chuyển động và lực tác dụng lên các vật thể. Trong Khoa học máy tính, vectơ được sử dụng để biểu diễn các điểm, đường thẳng, mặt phẳng trong không gian ba chiều.
Để học tốt môn Toán 11, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn đã cung cấp, các em sẽ tự tin hơn khi giải bài 9 trang 24 Chuyên đề học tập Toán 11 Cánh diều và đạt kết quả tốt trong môn Toán.