Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 43 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu sâu hơn về kiến thức đã học.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác, dễ hiểu và đầy đủ.
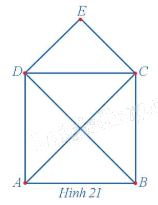
Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Hamilton (nếu có) của đồ thị ở Hình 21.
Đề bài
Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Hamilton (nếu có) của đồ thị ở Hình 21.
Phương pháp giải - Xem chi tiết
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần. Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết
Ta có: d(A) = 3, d(B) = 3, d(C) = 4, d(D) = 4, d(E) = 2.
Vì đồ thị ở Hình 21 gồm có 5 đỉnh nên tổng bậc của hai đỉnh không kề nhau bất kì đều không nhỏ hơn 5. Do đó, theo định lí Ore, đồ thị này có ít nhất một chu trình Hamilton.
Một chu trình Hamilton của đồ thị này là ABCEDA.
Bài 4 trang 43 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 43 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, học sinh cần:
Bài toán: Cho hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, tìm điểm cực trị và vẽ đồ thị hàm số.
Giải:
Khi giải bài 4 trang 43 Chuyên đề học tập Toán 11 Cánh diều, học sinh cần lưu ý:
Bài 4 trang 43 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và sử dụng các phương pháp giải hiệu quả, học sinh có thể giải quyết bài tập này một cách tự tin và đạt kết quả tốt.