Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 47, 48 Chuyên đề học tập Toán 11 - Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi luôn cố gắng mang đến những phương pháp giải bài tập hiệu quả nhất, giúp các em học toán một cách dễ dàng và thú vị.
Hexane C6H14 có năm đồng phân. Vẽ đồ thị tương ứng với năm đồng phân đó.
Đề bài
Hexane C6H14 có năm đồng phân. Vẽ đồ thị tương ứng với năm đồng phân đó.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đồng phân trong Hóa học để làm
Lời giải chi tiết
Năm đồng phân của hexane C6H14 là:
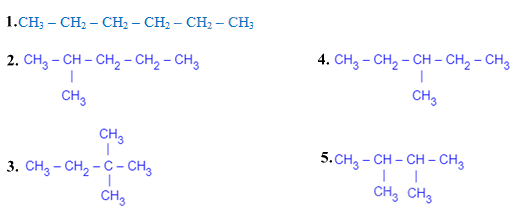
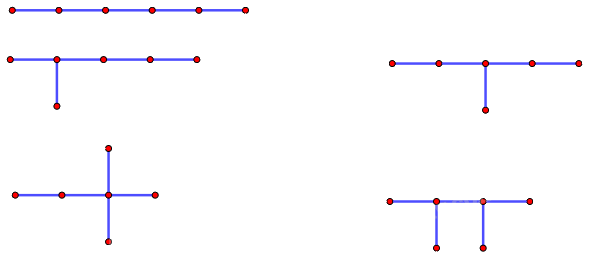
Các đồ thị ở hình dưới đây tương ứng minh họa biểu diễn năm đồng phân của hexane C6H14. Trong đó các nguyên tử C, CH, CH2, CH3 tạo nên các đỉnh của đồ thị, còn các liên kết CH3 – CH2, CH2 – CH2, CH2 – CH3, CH3 – CH, CH – CH3, CH – CH2, CH2 – C, C – CH3, CH2 – CH, CH – CH tạo nên các cạnh của đồ thị.
Mục 2 của Chuyên đề học tập Toán 11 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để giải quyết các bài tập một cách hiệu quả. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 47, 48, đồng thời phân tích các phương pháp giải và lưu ý quan trọng.
Trước khi đi vào giải bài tập, chúng ta cần xác định rõ nội dung chính của Mục 2. Thông thường, mục này sẽ đề cập đến các khái niệm, định lý, và tính chất quan trọng liên quan đến một chủ đề cụ thể. Ví dụ, nếu Mục 2 nói về hàm số bậc hai, thì các em cần nắm vững các kiến thức về:
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập trang 47. Đối với mỗi bài tập, chúng ta sẽ:
Đề bài: Xác định hệ số a, b, c của hàm số y = 2x2 - 5x + 3.
Lời giải:
So sánh hàm số y = 2x2 - 5x + 3 với dạng tổng quát y = ax2 + bx + c, ta có:
Tương tự như trang 47, chúng ta sẽ giải chi tiết các bài tập trang 48. Lưu ý rằng, một số bài tập có thể yêu cầu các em vận dụng kiến thức từ nhiều chủ đề khác nhau. Do đó, hãy đảm bảo rằng các em đã nắm vững kiến thức nền tảng trước khi bắt đầu giải bài tập.
Đề bài: Tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Lời giải:
Tọa độ đỉnh của parabol y = ax2 + bx + c được tính theo công thức:
xđỉnh = -b / 2a
yđỉnh = -Δ / 4a (với Δ = b2 - 4ac)
Trong trường hợp này, a = 1, b = -4, c = 3. Do đó:
Vậy tọa độ đỉnh của parabol là (2; -1).
Để giải bài tập Toán 11 - Cánh diều một cách hiệu quả, các em cần lưu ý những điều sau:
Hy vọng rằng, với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập trong Mục 2 trang 47, 48 Chuyên đề học tập Toán 11 - Cánh diều. Chúc các em học tập tốt!