Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm
Đề bài
Chứng minh rằng nếu phép dời hình F biến tam giác ABC thành tam giác A'B'C' thì F lần lượt biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các phép biến hình để trả lời
Lời giải chi tiết
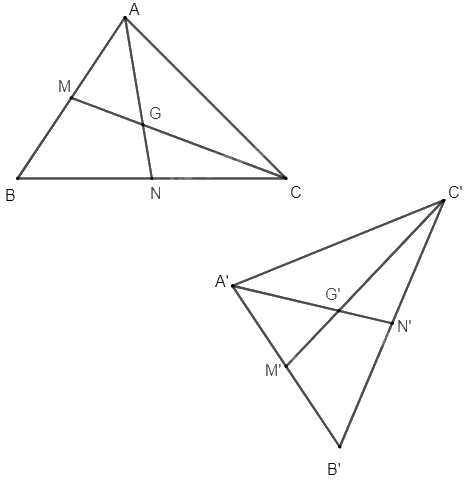
+) Phép dời hình F biến tam giác ABC thành tam giác A'B'C', do đó F biến các đoạn thẳng AB, BC tương ứng thành các đoạn thẳng A'B', B'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, BC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', B'C'. Vậy F biến các trung tuyến CM, AN của tam giác ABC tương ứng thành các trung tuyến C'M', A'N' của tam giác A'B'C'. Từ đó suy ra F biến trọng tâm G của tam giác ABC là giao của CM và AN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và A'N'.
+) Gọi AH là đường cao của tam giác ABC (H ∈ BC). Khi đó phép dời hình F biến đường thẳng AH thành đường thẳng A'H'. Vì AH ⊥ BC nên A'H' ⊥ B'C', nói cách khác A'H' là đường cao của tam giác A'B'C'. Đối với các đường cao khác cũng thế. Vì trực tâm tam giác là giao điểm của các đường cao nên trực tâm tam giác ABC biến thành trực tâm tam giác A'B'C'.
+) Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC thì OA = OB = OC nên nếu điểm O biến thành điểm O' qua phép dời hình F thì O'A' = O'B' = O'C' = OA = OB = OC, do đó O' là tâm đường tròn ngoại tiếp tam giác A'B'C'.
Bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Bài 15 thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài tập: Xét hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, khoảng đồng biến, khoảng nghịch biến và vẽ đồ thị hàm số.
Giải:
Khi giải bài tập về hàm số, bạn cần chú ý đến các điểm sau:
Bài 15 trang 25 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đồ thị hàm số. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải hiệu quả và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài tập tương tự.