Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 6 trang 21, 22 Chuyên đề học tập Toán 11 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm \(I\left( {--{\rm{ }}3;{\rm{ }}2} \right)\) bán kính \(R{\rm{ }} = {\rm{ }}1\). Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\). Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó viết phương trình (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng tâm O là một đường tròn có bán kính bằng 1, gọi là (C').
Gọi I' là tâm của đường tròn (C'), khi đó I' là ảnh của I qua phép đối xứng tâm O. Suy ra I'(3; – 2). Do vậy, đường tròn (C') có tâm I'(3; – 2) và bán kính bằng 1.
Ảnh của đường tròn (C') qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) một đường tròn có bán kính bằng 1, gọi là (C").
Gọi I" là tâm của đường tròn (C"), khi đó I" là ảnh của I' qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) suy ra nên I"(2; 1). Do vậy, đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Vậy ảnh của đường tròn (C) qua phép dời hình f là đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
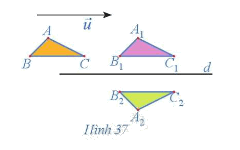
Quan sát Hình 37.
a) Chỉ ra các phép dời hình biến tam giác ABC thành tam giác A1B1C1 và biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Có nhận xét gì về hai tam giác ABC và \({A_2}{B_2}{C_2}?\)
Phương pháp giải:
Quan sát hình 37 và dựa vào kiến thức tịnh tiến, đối xứng trục để làm
Lời giải chi tiết:
) Quan sát Hình 37, ta thấy phép tịnh tiến theo vectơ \(\vec u\) biến tam giác ABC thành tam giác A1B1C1 và phép đối xứng trục d biến biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Theo tính chất của phép tịnh tiến và phép đối xứng trục, ta suy ra
\(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2},{\rm{ }}BC{\rm{ }} = {\rm{ }}{B_1}{C_1}\; = {\rm{ }}{B_2}{C_2},{\rm{ }}AC{\rm{ }} = {\rm{ }}{A_1}{C_1}\; = {\rm{ }}{A_2}{C_2}.\)
Do đó, hai tam giác ABC và \({A_2}{B_2}{C_2}\) bằng nhau.
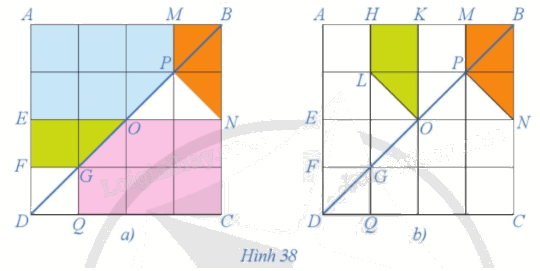
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.
Phương pháp giải:
Quan sát hình 38 và dựa vào kiến thức:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Quan sát hình ta thấy \(OA{\rm{ }} = {\rm{ }}OC,{\rm{ }}OM{\rm{ }} = {\rm{ }}OQ,{\rm{ }}OP{\rm{ }} = {\rm{ }}OG,{\rm{ }}OE{\rm{ }} = {\rm{ }}ON\) nên O là trung điểm của các đoạn thẳng AC, MQ, PG, EN. Do đó, ta có phép đối xứng tâm O biến các điểm A, M, P, O, E tương ứng thành các điểm C, Q, G, O, N. Như vậy, phép đối xứng tâm O biến hình AMPOE thành hình CQGON. Vậy hai hình AMPOE và CQGON bằng nhau.
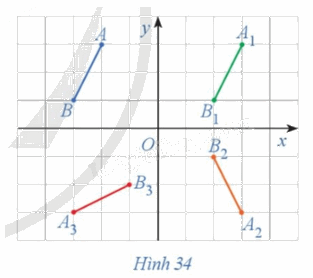
Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
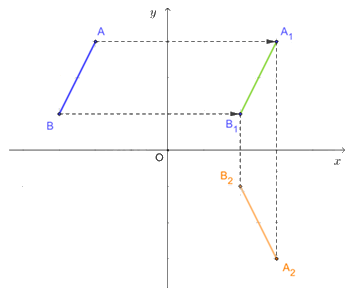
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\);
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox;
c) Đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay \(\;\varphi = --90^\circ ;\)
d) So sánh độ dài các đoạn thẳng \(AB,{\rm{ }}{A_1}{B_1},{\rm{ }}{A_2}{B_2},{\rm{ }}{A_3}{B_3}.\)
Phương pháp giải:
Quan sát hình 34 và dựa vào định nghĩa:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
a) Lấy điểm M, sao cho M(5; 0). Khi đó \(\overrightarrow {OM} = \left( {5;\,0} \right) = \vec u\).
Lấy các điểm A1 và B1 sao cho \(\overrightarrow {A{A_1}} = \overrightarrow {OM} ,\,\overrightarrow {B{B_1}} = \overrightarrow {OM} \). Khi đó \(\overrightarrow {{\rm{A}}{{\rm{A}}_1}} = \overrightarrow {B{B_1}} = \vec u\) nên A1, B1 lần lượt là ảnh của A, B qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\). Vậy đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\).
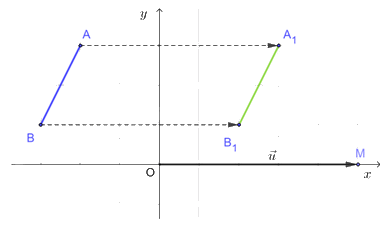
b) Từ A1, kẻ đường thẳng vuông góc với Ox, trên đường thẳng này lấy A2 khác phía với A1 đối với Ox sao cho khoảng cách từ A1 đến Ox bằng khoảng cách từ A2 tới Ox. Khi đó Ox là đường trung trực của đoạn thẳng A1A2.
Tương tự, dựng B2 sao cho Ox là đường trung trực của đoạn thẳng B1B2.
Khi đó ta có phép đối xứng trục Ox biến các điểm A1, B1 tương ứng thành các điểm A2, B2. Vậy đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox.
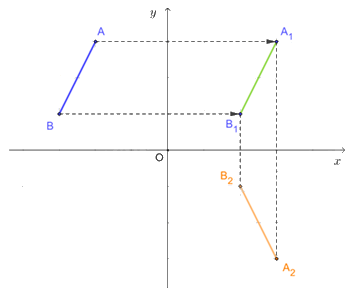
c) Phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.
Qua O, vẽ đường thẳng vuông góc với \(O{A_2}\), trên đường thẳng này lấy điểm \({A_3}\) sao cho \(O{A_2}\; = {\rm{ }}O{A_3}\;\) và góc quay từ A2 đến A3 theo chiều kim đồng hồ. Khi đó A3 là ảnh của điểm A2 qua phép quay tâm O, góc quay – 90°. Tương tự, xác định được điểm B3 là ảnh của điểm B2 qua phép quay tâm O, góc quay – 90°. Vậy đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay \(\varphi = --90^\circ .\)
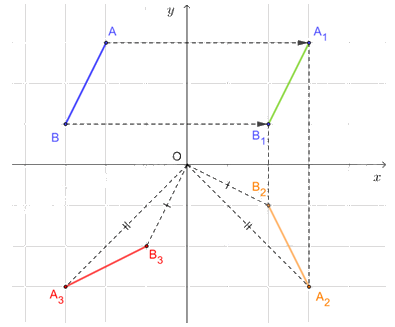
d) Vì phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì nên \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Vì phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}.\)
Vì phép quay bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)Do đó, \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)
Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\);
b) Đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox;
c) Đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay \(\;\varphi = --90^\circ ;\)
d) So sánh độ dài các đoạn thẳng \(AB,{\rm{ }}{A_1}{B_1},{\rm{ }}{A_2}{B_2},{\rm{ }}{A_3}{B_3}.\)
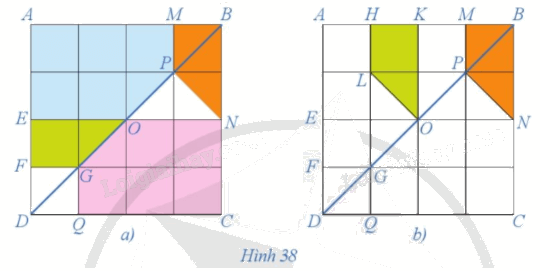
Phương pháp giải:
Quan sát hình 34 và dựa vào định nghĩa:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
a) Lấy điểm M, sao cho M(5; 0). Khi đó \(\overrightarrow {OM} = \left( {5;\,0} \right) = \vec u\).
Lấy các điểm A1 và B1 sao cho \(\overrightarrow {A{A_1}} = \overrightarrow {OM} ,\,\overrightarrow {B{B_1}} = \overrightarrow {OM} \). Khi đó \(\overrightarrow {{\rm{A}}{{\rm{A}}_1}} = \overrightarrow {B{B_1}} = \vec u\) nên A1, B1 lần lượt là ảnh của A, B qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\). Vậy đoạn thẳng A1B1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\).
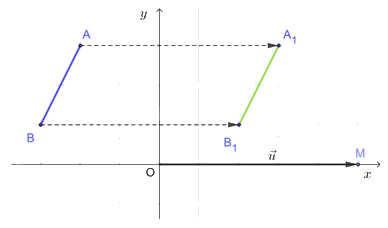
b) Từ A1, kẻ đường thẳng vuông góc với Ox, trên đường thẳng này lấy A2 khác phía với A1 đối với Ox sao cho khoảng cách từ A1 đến Ox bằng khoảng cách từ A2 tới Ox. Khi đó Ox là đường trung trực của đoạn thẳng A1A2.
Tương tự, dựng B2 sao cho Ox là đường trung trực của đoạn thẳng B1B2.
Khi đó ta có phép đối xứng trục Ox biến các điểm A1, B1 tương ứng thành các điểm A2, B2. Vậy đoạn thẳng A2B2 là ảnh của đoạn thẳng A1B1 qua phép đối xứng trục Ox.
c) Phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.
Qua O, vẽ đường thẳng vuông góc với \(O{A_2}\), trên đường thẳng này lấy điểm \({A_3}\) sao cho \(O{A_2}\; = {\rm{ }}O{A_3}\;\) và góc quay từ A2 đến A3 theo chiều kim đồng hồ. Khi đó A3 là ảnh của điểm A2 qua phép quay tâm O, góc quay – 90°. Tương tự, xác định được điểm B3 là ảnh của điểm B2 qua phép quay tâm O, góc quay – 90°. Vậy đoạn thẳng A3B3 là ảnh của đoạn thẳng A2B2 qua phép quay tâm O với góc quay \(\varphi = --90^\circ .\)
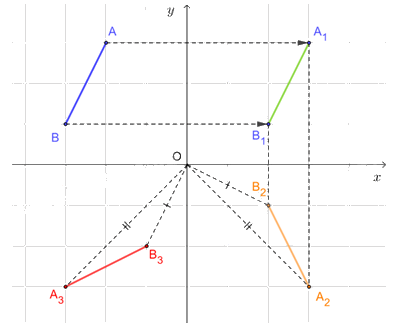
d) Vì phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì nên \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Vì phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}.\)
Vì phép quay bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)Do đó, \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm \(I\left( {--{\rm{ }}3;{\rm{ }}2} \right)\) bán kính \(R{\rm{ }} = {\rm{ }}1\). Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\). Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó viết phương trình (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng tâm O là một đường tròn có bán kính bằng 1, gọi là (C').
Gọi I' là tâm của đường tròn (C'), khi đó I' là ảnh của I qua phép đối xứng tâm O. Suy ra I'(3; – 2). Do vậy, đường tròn (C') có tâm I'(3; – 2) và bán kính bằng 1.
Ảnh của đường tròn (C') qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) một đường tròn có bán kính bằng 1, gọi là (C").
Gọi I" là tâm của đường tròn (C"), khi đó I" là ảnh của I' qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) suy ra nên I"(2; 1). Do vậy, đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Vậy ảnh của đường tròn (C) qua phép dời hình f là đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
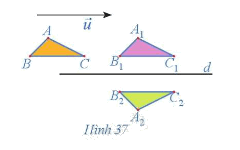
Quan sát Hình 37.
a) Chỉ ra các phép dời hình biến tam giác ABC thành tam giác A1B1C1 và biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Có nhận xét gì về hai tam giác ABC và \({A_2}{B_2}{C_2}?\)
Phương pháp giải:
Quan sát hình 37 và dựa vào kiến thức tịnh tiến, đối xứng trục để làm
Lời giải chi tiết:
) Quan sát Hình 37, ta thấy phép tịnh tiến theo vectơ \(\vec u\) biến tam giác ABC thành tam giác A1B1C1 và phép đối xứng trục d biến biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Theo tính chất của phép tịnh tiến và phép đối xứng trục, ta suy ra
\(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2},{\rm{ }}BC{\rm{ }} = {\rm{ }}{B_1}{C_1}\; = {\rm{ }}{B_2}{C_2},{\rm{ }}AC{\rm{ }} = {\rm{ }}{A_1}{C_1}\; = {\rm{ }}{A_2}{C_2}.\)
Do đó, hai tam giác ABC và \({A_2}{B_2}{C_2}\) bằng nhau.
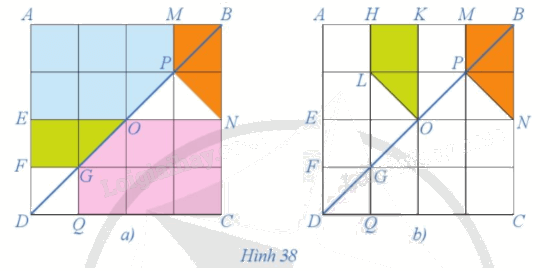
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.
Phương pháp giải:
Quan sát hình 38 và dựa vào kiến thức:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Quan sát hình ta thấy \(OA{\rm{ }} = {\rm{ }}OC,{\rm{ }}OM{\rm{ }} = {\rm{ }}OQ,{\rm{ }}OP{\rm{ }} = {\rm{ }}OG,{\rm{ }}OE{\rm{ }} = {\rm{ }}ON\) nên O là trung điểm của các đoạn thẳng AC, MQ, PG, EN. Do đó, ta có phép đối xứng tâm O biến các điểm A, M, P, O, E tương ứng thành các điểm C, Q, G, O, N. Như vậy, phép đối xứng tâm O biến hình AMPOE thành hình CQGON. Vậy hai hình AMPOE và CQGON bằng nhau.
Mục 6 của Chuyên đề học tập Toán 11 - Cánh diều tập trung vào các kiến thức về đạo hàm của hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho việc học các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các công thức đạo hàm lượng giác và cách áp dụng chúng vào giải bài tập là điều cần thiết để đạt kết quả tốt trong môn Toán.
Mục 6 bao gồm các nội dung chính sau:
Trang 21 tập trung vào việc vận dụng các công thức đạo hàm lượng giác cơ bản để tính đạo hàm của các hàm số đơn giản. Các bài tập thường yêu cầu tính đạo hàm của các biểu thức như sin(2x), cos(x^2), tan(3x),... Để giải các bài tập này, các em cần nắm vững các công thức đạo hàm và quy tắc đạo hàm hàm hợp.
Áp dụng quy tắc đạo hàm hàm hợp, ta có:
y' = cos(2x) * (2x)' = 2cos(2x)
Áp dụng quy tắc đạo hàm hàm hợp, ta có:
y' = -sin(x^2) * (x^2)' = -2xsin(x^2)
Trang 22 nâng cao độ khó bằng cách yêu cầu tính đạo hàm của các hàm số phức tạp hơn, kết hợp nhiều phép toán và các hàm số lượng giác khác nhau. Các bài tập thường yêu cầu sử dụng các công thức đạo hàm lượng giác và quy tắc đạo hàm hàm hợp một cách linh hoạt.
y' = (tan(x))' + (sin(x))' = 1/cos^2(x) + cos(x)
Áp dụng quy tắc đạo hàm của tích, ta có:
y' = (sin(x))' * cos(x) + sin(x) * (cos(x))' = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos^2(x) - sin^2(x)
Để hiểu sâu hơn về đạo hàm lượng giác, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm lượng giác trong Mục 6 trang 21, 22 Chuyên đề học tập Toán 11 - Cánh diều. Chúc các em học tập tốt!