Bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.
Đề bài
Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.
a) Xác định ảnh của các điểm D và C quay phép quay tâm A với góc quay \(\varphi = 60^\circ .\)
b) Chứng minh rằng DC = BE.
c) Chứng minh rằng số đo góc giữa hai đường thẳng DC và BE bằng 60°.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức phép quay:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
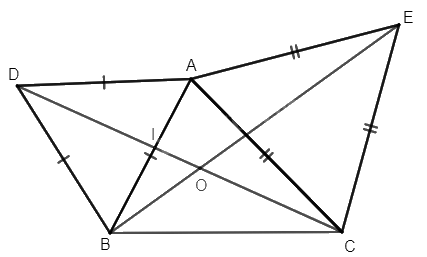
a) + Vì tam giác ABD đều nên AD = AB và \(\widehat {DAB} = 60^\circ \).
Phép quay với góc quay φ = 60° có chiều quay ngược chiều kim đồng hồ. Do đó, ảnh của điểm D phép quay tâm A với góc quay \(\varphi = 60^\circ \) là điểm B.
+ Vì tam giác ACE đều nên AC = AE và \(\widehat {CAE} = 60^\circ \).
Do đó, ảnh của điểm C phép quay tâm A với góc quay \(\varphi = 60^\circ \) là điểm E.
b) Theo câu a) ta có B và E lần lượt là ảnh của D và C qua phép quay tâm A với góc quay \(\varphi = 60^\circ \), suy ra DC = BE (phép quay bảo toàn khoảng cách giữa hai điểm bất kì).
c) Gọi O là giao điểm của DC và BE, I là giao điểm của AB và DC.
Ta có phép quay tâm A với góc quay φ = 60° biến góc ADC thành góc ABE nên \(\widehat {ADC} = \widehat {ABE}\) hay \(\widehat {ADI} = \widehat {IBO}\).
Mà \(\widehat {AID} = \widehat {BIO}\) (2 góc đối đỉnh), \(\widehat {ADI} + \widehat {AID} + \widehat {DAI} = 180^\circ \) (tổng ba góc trong tam giác ADI) và \(\widehat {IBO} + \widehat {BIO} + \widehat {IOB} = 180^\circ \) (tổng ba góc trong tam giác IBO).
Từ đó suy ra \(\widehat {DAI} = \widehat {IOB}\) hay \(\widehat {DOB} = \widehat {DAB} = 60^\circ \).
Như vậy, số đo góc giữa hai đường thẳng DC và BE bằng 60°.
Bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này tập trung vào việc ứng dụng đạo hàm để tìm cực trị của hàm số, xét tính đơn điệu của hàm số và giải các bài toán liên quan đến tối ưu hóa.
Bài 13 thường bao gồm các dạng bài tập sau:
Để giải bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm cấp nhất: f'(x) = 3x2 - 6x.
Bước 2: Tìm các điểm dừng: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
Bước 3: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Kết luận: Hàm số f(x) đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.