Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 5, 6 Chuyên đề học tập Toán 11 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Chuyên đề học tập Toán 11 - Cánh diều là một tài liệu quan trọng giúp các em ôn luyện và củng cố kiến thức. Việc giải các bài tập trong chuyên đề này sẽ giúp các em hiểu sâu hơn về các khái niệm và phương pháp giải toán.
Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc M' của điểm M lên đường thẳng d (Hình 2).
Đề bài
Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc M' của điểm M lên đường thẳng d (Hình 2).
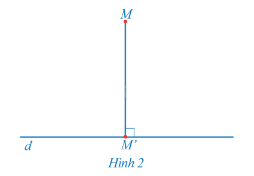
a) Có bao nhiêu hình chiếu vuông góc của điểm M trên đường thẳng d?
b) Có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d hay không?
Phương pháp giải - Xem chi tiết
Quan sát hình 2 để trả lời
Lời giải chi tiết
a) Với mỗi điểm M có một điểm M' duy nhất là hình chiếu vuông góc của điểm M trên đường thẳng d cho trước.
b) Không có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d.
Mục 1 của Chuyên đề học tập Toán 11 - Cánh diều tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc hai. Đây là một phần kiến thức nền tảng quan trọng, xuất hiện thường xuyên trong các bài kiểm tra và kỳ thi. Việc nắm vững các khái niệm, tính chất và phương pháp giải toán liên quan đến hàm số bậc hai là điều cần thiết để đạt kết quả tốt trong môn Toán.
Dưới đây là lời giải chi tiết các bài tập trong mục 1 trang 5, 6 Chuyên đề học tập Toán 11 - Cánh diều:
Ta có y' = 2x - 4. Cho y' = 0, ta được x = 2. Khi x < 2, y' < 0, hàm số nghịch biến. Khi x > 2, y' > 0, hàm số đồng biến. Vậy hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).
Hàm số có dạng y = ax² + bx + c với a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = -6/(2*(-1)) = 3. Tung độ đỉnh là y = -3² + 6*3 - 5 = 4. Vậy giá trị lớn nhất của hàm số là 4.
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, các em cần:
Việc học toán không chỉ là việc học thuộc công thức mà còn là việc hiểu bản chất của vấn đề. Hãy cố gắng suy nghĩ và tìm tòi để giải quyết các bài tập một cách độc lập. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô hoặc bạn bè. Chúc các em học tốt!
| Bài tập | Phương pháp giải |
|---|---|
| Tìm tập xác định | Xác định điều kiện để hàm số có nghĩa |
| Xét tính đơn điệu | Sử dụng đạo hàm |
| Tìm giá trị lớn nhất/nhỏ nhất | Sử dụng đạo hàm hoặc phương pháp hoành độ đỉnh |