Bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
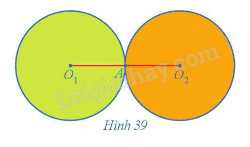
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
Đề bài
Cho hai đường tròn (O1; R) và (O2; R) tiếp xúc ngoài với nhau tại A (Hình 39).
a) Tìm phép tịnh tiến biến đường tròn (O1) thành đường tròn (O2).
b) Tìm phép đối xứng tâm biến đường tròn (O1) thành đường tròn (O2).
c) Tìm phép đối xứng trục biến đường tròn (O1) thành đường tròn (O2).
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức:
- Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \({Đ_d}\).
Lời giải chi tiết
a) Hai đường tròn \(({O_1};{\rm{ }}R)\) và \(({O_2};{\rm{ }}R)\) có cùng bán kính. Ta có phép tịnh tiến theo vectơ \(\overrightarrow {{O_1}{O_2}} \) biến điểm tâm \({O_1}\) thành tâm \({O_2}\).
Như vậy, phép tịnh tiến theo vectơ \(\overrightarrow {{O_1}{O_2}} \) biến đường tròn \(({O_1};{\rm{ }}R)\)thành đường tròn \(({O_2};{\rm{ }}R)\)
b) Ta có: \({O_1}A{\rm{ }} = {\rm{ }}{O_2}A{\rm{ }} = {\rm{ }}R\) nên A là trung điểm của \({O_1}{O_2}\). Do đó, có phép đối xứng tâm A biến O1 thành O2.
Như vậy, phép đối xứng tâm O biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}R)\).
c)
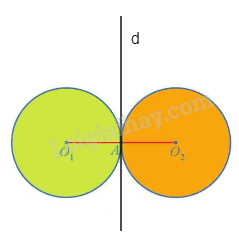
Qua A, kẻ đường thẳng d vuông góc với \({O_1}{O_2}.\)Khi đó đường thẳng d là đường trung trực của đoạn thẳng O1O2. Do đó, ta có phép đối xứng trục d biến O1 thành O2.
Như vậy, phép đối xứng trục d biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}R)\).
Bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều, học sinh cần xác định hàm số được cho, các điều kiện ràng buộc và mục tiêu cần đạt được. Việc phân tích đề bài một cách cẩn thận sẽ giúp học sinh tránh được những sai sót không đáng có và tìm ra hướng giải quyết hiệu quả.
Để giải bài tập hàm số và đồ thị, học sinh cần nắm vững các kiến thức cơ bản về hàm số, bao gồm:
Ngoài ra, học sinh cũng cần thành thạo các kỹ năng vẽ đồ thị hàm số, sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị.
(Giả sử bài 5 là một bài toán cụ thể về hàm số bậc hai. Nội dung sau đây sẽ là lời giải chi tiết cho bài toán đó.)
Bài 5: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.
Lời giải:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
Hoành độ đỉnh: x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh: y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2; -1).
Xác định một vài điểm thuộc đồ thị hàm số, ví dụ:
Vẽ parabol đi qua các điểm đã xác định và có đỉnh là (2; -1).
Để củng cố kiến thức và kỹ năng giải bài tập hàm số và đồ thị, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Kiến thức về hàm số và đồ thị có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kinh tế, kỹ thuật, khoa học tự nhiên. Ví dụ, trong kinh tế, hàm số có thể được sử dụng để mô tả mối quan hệ giữa cung và cầu, chi phí và doanh thu. Trong kỹ thuật, đồ thị có thể được sử dụng để biểu diễn các thông số kỹ thuật của một thiết bị hoặc hệ thống.
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh có thể tự tin giải bài 5 trang 24 Chuyên đề học tập Toán 11 Cánh diều và đạt kết quả tốt trong môn Toán.