Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, phương pháp giải và tự tin hơn trong quá trình học tập môn Toán.

Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn lời giải bài 6 trang 24 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.

Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.

Đề bài

Trong Hình 40, hình màu xanh là ảnh của hình màu cam qua một phép quay. Xác định tâm và góc quay của phép quay đó.

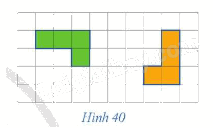
Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều 2

Xác định tâm và góc quay dựa vào định nghĩa:

Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.

Lời giải chi tiết

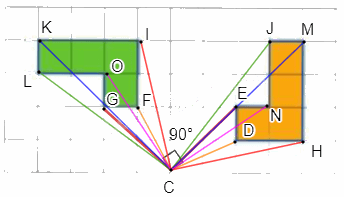
Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều 3

Ta thấy:

+)\(CH{\rm{ }} = {\rm{ }}CI,{\rm{ }}CM{\rm{ }} = {\rm{ }}CK,{\rm{ }}CJ{\rm{ }} = {\rm{ }}CL,{\rm{ }}CN{\rm{ }} = {\rm{ }}CO,{\rm{ }}CE{\rm{ }} = {\rm{ }}CG,{\rm{ }}CD{\rm{ }} = {\rm{ }}CF\;\) (đường chéo của các hình chữ nhật có cùng kích thước).

+) \(\widehat {HCI} = \widehat {MCK} = \widehat {JCL} = \widehat {NCO} = \widehat {ECG} = \widehat {DCF} = 90^\circ \).

Do đó, ta có phép quay tâm C, góc quay 90° biến các điểm H, M, J, N, E, D tương ứng thành các điểm I, K, L, O, G, F.

Như vậy, hình màu xanh là ảnh của hình màu cam quay phép quay tâm C, góc quay 90°.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Học tốt Toán lớp 11 trên nền tảng đề thi toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều: Tổng quan

Bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích, suy luận và áp dụng các công thức, định lý đã học để tìm ra đáp án chính xác.

Nội dung chi tiết bài 6 trang 24

Để giải quyết bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:

Hàm số bậc hai: Định nghĩa, dạng tổng quát, đồ thị hàm số, các yếu tố của đồ thị (đỉnh, trục đối xứng, giao điểm với các trục tọa độ).
Các phép biến đổi hàm số: Tịnh tiến, đối xứng, co giãn theo phương ngang và phương dọc.
Điều kiện xác định của hàm số: Xác định tập xác định của hàm số, các giá trị không xác định.
Phương pháp giải: Phân tích bài toán, lựa chọn phương pháp giải phù hợp, kiểm tra lại kết quả.

Hướng dẫn giải chi tiết bài 6 trang 24

Dưới đây là hướng dẫn giải chi tiết bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các giải thích chi tiết để bạn có thể nắm vững phương pháp giải.

Phần 1: Phân tích đề bài

Đầu tiên, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các thông tin đã cho và các thông tin cần tìm. Phân tích mối quan hệ giữa các yếu tố trong bài toán.

Phần 2: Lựa chọn phương pháp giải

Dựa trên phân tích đề bài, chúng ta lựa chọn phương pháp giải phù hợp. Có thể sử dụng các phương pháp như:

Phương pháp đại số: Sử dụng các công thức, định lý để giải phương trình, bất phương trình.
Phương pháp hình học: Sử dụng các tính chất hình học để giải bài toán.
Phương pháp đồ thị: Sử dụng đồ thị hàm số để tìm ra đáp án.

Phần 3: Thực hiện giải bài toán

Thực hiện giải bài toán theo phương pháp đã lựa chọn. Trình bày các bước giải một cách rõ ràng, logic. Kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Để giúp bạn hiểu rõ hơn về cách giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều, chúng ta sẽ xem xét một ví dụ minh họa cụ thể.

Ví dụ: Cho hàm số y = x² - 4x + 3. Tìm tọa độ đỉnh của parabol.

Giải:

Xác định hệ số a, b, c của hàm số: a = 1, b = -4, c = 3.
Tính hoành độ đỉnh: x_đỉnh = -b / (2a) = -(-4) / (2 * 1) = 2.
Tính tung độ đỉnh: y_đỉnh = f(x_đỉnh) = f(2) = 2² - 4 * 2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2; -1).

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều, bạn có thể luyện tập thêm với các bài tập tương tự. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học Toán online.

Kết luận

Bài 6 trang 24 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức về hàm số. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn đã có thể tự tin giải quyết bài toán một cách hiệu quả.

Chúc bạn học tập tốt!