Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 14, 15, 16 Chuyên đề học tập Toán 11 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp các em hiểu sâu sắc bản chất của từng bài toán.
Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1).
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng tâm S (2;1) bằng cách:
Nếu \(M'{\rm{ }} = {\rm{ }}{D_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Sau đó xác định ảnh của đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của điểm I qua phép đối xứng tâm S(2; 1). Suy ra S là trung điểm của II'. Do đó \(\left\{ {\begin{array}{*{20}{l}}{{x_{I'}} = 2{x_S} - {x_I} = 2.2 - 2 = 2}\\{{y_{I'}} = 2{y_S} - {y_I} = 2.1 - 3 = - 1}\end{array}} \right.\)nên I'(2; – 1).
Vậy ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là đường tròn (C') có tâm I'(2;– 1) và bán kính R' = 2.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng tâm O.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{D_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Trong mặt phẳng tọa độ Oxy, điểm M'(x1'; y1') là ảnh của điểm M(x1; y1) qua phép đối xứng tâm O, khi đó \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = - {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
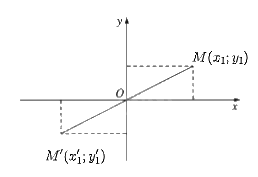
Do đó, M'(– x1; – y1) và N'(– x2; – y2).
b) Ta có:
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = \sqrt {{{\left( { - \left( {{x_2} - {x_1}} \right)} \right)}^2} + {{\left( { - \left( {{y_2} - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
Cho bát giác đều ABCDEGHK với tâm I. Xác định ảnh của các điểm A, B, C, D qua phép đối xứng tâm I.
Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
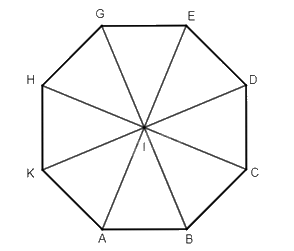
Vì I là tâm của bát giác đều ABCDEGHK nên I là trung điểm của các đoạn thẳng AE, BG, CH, DK. Suy ra ảnh của các điểm A, B, C, D qua phép đối xứng tâm I lần lượt là các điểm E, G, H, K.
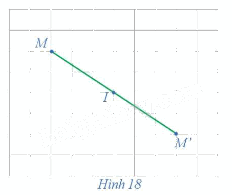
Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).
Phương pháp giải:
Với mỗi điểm M bất kì, xác định M' sao cho I là trung điểm của MM', từ đó rút ra kết luận
Lời giải chi tiết:
Cách xác định:
Lấy điểm I trong mặt phẳng, với mỗi điểm M bất kì, ta vẽ đường thẳng MI, trên đường thẳng này, ta lấy điểm M' sao cho MI = M'I và điểm I nằm giữa hai điểm M và M'. Khi đó I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I).
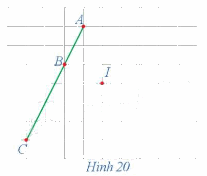
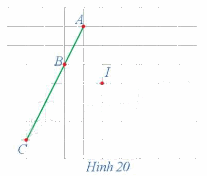
Xét phép đối xứng tâm I (Hình 20).
a) Xác định các điểm A', B', C' là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I như trên hình vẽ dưới đây.
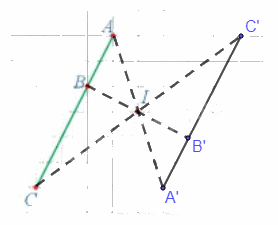
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
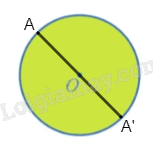
Trong mặt phẳng, cho hình tròn tâm O, kí hiệu là ℋ (Hình 22). Xét phép đối xứng tâm ĐO. Tìm ℋ' = ĐO(ℋ).

Phương pháp giải:
Tìm ảnh của (H) qua ĐO bằng cách tìm ảnh của các điểm thuộc (H) qua ĐO. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
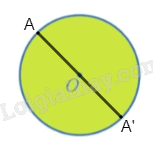
Với mỗi điểm A bất kì thuộc đường tròn tâm O, gọi A' là ảnh của A qua phép đối xứng tâm O. Khi đó O là trung điểm của AA' nên AA' là đường kính của đường tròn tâm O, suy ra A' thuộc đường tròn tâm O.
Như vậy, với mỗi điểm bất kì thuộc đường tròn tâm O, ta đều có ảnh của nó qua phép đối xứng tâm O là một điểm cũng thuộc đường tròn tâm O. Do đó, phép đối xứng tâm O biến đường tròn tâm O thành đường tròn tâm O.
Vậy phép đối xứng tâm O viến hình ℋ thành chính nó hay ℋ ' ≡ ℋ.
Trong mặt phẳng cho điểm I. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I) (Hình 18).

Phương pháp giải:
Với mỗi điểm M bất kì, xác định M' sao cho I là trung điểm của MM', từ đó rút ra kết luận
Lời giải chi tiết:
Cách xác định:
Lấy điểm I trong mặt phẳng, với mỗi điểm M bất kì, ta vẽ đường thẳng MI, trên đường thẳng này, ta lấy điểm M' sao cho MI = M'I và điểm I nằm giữa hai điểm M và M'. Khi đó I là trung điểm của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua điểm I).
Cho bát giác đều ABCDEGHK với tâm I. Xác định ảnh của các điểm A, B, C, D qua phép đối xứng tâm I.
Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Vì I là tâm của bát giác đều ABCDEGHK nên I là trung điểm của các đoạn thẳng AE, BG, CH, DK. Suy ra ảnh của các điểm A, B, C, D qua phép đối xứng tâm I lần lượt là các điểm E, G, H, K.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng tâm O.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{D_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Trong mặt phẳng tọa độ Oxy, điểm M'(x1'; y1') là ảnh của điểm M(x1; y1) qua phép đối xứng tâm O, khi đó \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = - {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
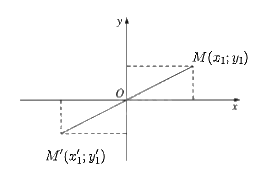
Do đó, M'(– x1; – y1) và N'(– x2; – y2).
b) Ta có:
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = \sqrt {{{\left( { - \left( {{x_2} - {x_1}} \right)} \right)}^2} + {{\left( { - \left( {{y_2} - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
Xét phép đối xứng tâm I (Hình 20).
a) Xác định các điểm A', B', C' là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép đối xứng tâm I như trên hình vẽ dưới đây.
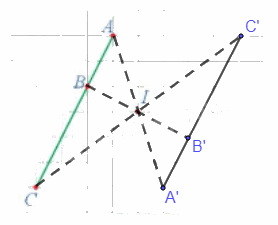
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1).
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng tâm S (2;1) bằng cách:
Nếu \(M'{\rm{ }} = {\rm{ }}{D_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Sau đó xác định ảnh của đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của điểm I qua phép đối xứng tâm S(2; 1). Suy ra S là trung điểm của II'. Do đó \(\left\{ {\begin{array}{*{20}{l}}{{x_{I'}} = 2{x_S} - {x_I} = 2.2 - 2 = 2}\\{{y_{I'}} = 2{y_S} - {y_I} = 2.1 - 3 = - 1}\end{array}} \right.\)nên I'(2; – 1).
Vậy ảnh của đường tròn (C) qua phép đối xứng tâm S(2; 1) là đường tròn (C') có tâm I'(2;– 1) và bán kính R' = 2.
Trong mặt phẳng, cho hình tròn tâm O, kí hiệu là ℋ (Hình 22). Xét phép đối xứng tâm ĐO. Tìm ℋ' = ĐO(ℋ).

Phương pháp giải:
Tìm ảnh của (H) qua ĐO bằng cách tìm ảnh của các điểm thuộc (H) qua ĐO. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
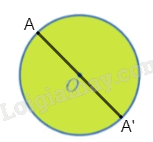
Với mỗi điểm A bất kì thuộc đường tròn tâm O, gọi A' là ảnh của A qua phép đối xứng tâm O. Khi đó O là trung điểm của AA' nên AA' là đường kính của đường tròn tâm O, suy ra A' thuộc đường tròn tâm O.
Như vậy, với mỗi điểm bất kì thuộc đường tròn tâm O, ta đều có ảnh của nó qua phép đối xứng tâm O là một điểm cũng thuộc đường tròn tâm O. Do đó, phép đối xứng tâm O biến đường tròn tâm O thành đường tròn tâm O.
Vậy phép đối xứng tâm O viến hình ℋ thành chính nó hay ℋ ' ≡ ℋ.
Mục 4 của Chuyên đề học tập Toán 11 - Cánh diều tập trung vào các kiến thức về phép biến hình. Đây là một phần quan trọng trong chương trình Toán 11, giúp học sinh hiểu rõ hơn về các phép biến hình cơ bản và ứng dụng của chúng trong hình học.
Trang 14 tập trung vào các bài tập về phép tịnh tiến. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép tịnh tiến. Để giải các bài tập này, học sinh cần nắm vững định nghĩa và tính chất của phép tịnh tiến.
Ví dụ: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.
Giải: A' = A + v = (1 + 3; 2 - 1) = (4; 1).
Trang 15 tập trung vào các bài tập về phép đối xứng trục. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng trục. Để giải các bài tập này, học sinh cần nắm vững định nghĩa và tính chất của phép đối xứng trục.
Ví dụ: Cho điểm B(-2; 3) và đường thẳng d: x + y - 1 = 0. Tìm ảnh B' của điểm B qua phép đối xứng trục d.
Giải: Bài toán này đòi hỏi học sinh phải tìm phương trình đường thẳng vuông góc với d và đi qua B, sau đó tìm giao điểm của hai đường thẳng này, và cuối cùng sử dụng công thức trung điểm để tìm B'.
Trang 16 tập trung vào các bài tập về phép đối xứng tâm và phép quay. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép đối xứng tâm hoặc phép quay. Để giải các bài tập này, học sinh cần nắm vững định nghĩa và tính chất của phép đối xứng tâm và phép quay.
Ví dụ: Cho điểm C(0; -4) và tâm đối xứng O(0; 0). Tìm ảnh C' của điểm C qua phép đối xứng tâm O.
Giải: C' = -C = (0; 4).
Phép biến hình có nhiều ứng dụng trong thực tế, chẳng hạn như trong thiết kế đồ họa, kiến trúc, robot học và nhiều lĩnh vực khác. Việc hiểu rõ về phép biến hình giúp học sinh có thể áp dụng kiến thức vào giải quyết các vấn đề thực tế.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập về phép biến hình. Chúc các em học tốt!