Bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 4 trang 23, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
Đề bài
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Xét phép đối xứng tâm O, xác định ảnh của:
a) Trung điểm các cạnh AB, BC, CD, DA;
b) Các đường thẳng AB, AC.
Phương pháp giải - Xem chi tiết
Dựa vào phép đối xứng tâm:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết
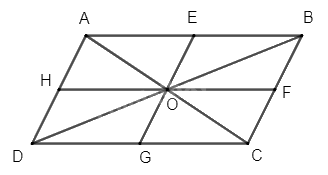
a) Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét tam giác ABC có E và O lần lượt là trung điểm của AB và AC nên OE là đường trung bình của tam giác ABC, suy ra OE // BC và \(OE = \frac{1}{2}BC\,\,(1)\)
Xét tam giác DBC có O và G lần lượt là trung điểm của DB và DC nên OG là đường trung bình của tam giác DBC, suy ra OG // BC và \(OG = \frac{1}{2}BC\,\,(2)\)
Từ (1) và (2) suy ra E, O, G thẳng hàng và OE = OG. Do đó, O là trung điểm của EG.
Chứng minh tương tự ta được O là trung điểm của HF.
Như vậy, ảnh của các điểm E, F, G, H qua phép đối xứng tâm O lần lượt là các điểm G, H, E, F.
b) Vì O là trung điểm của AC và BD nên ta có phép đối xứng tâm O biến các điểm A, B, C thành các điểm C, D, A.
Do đó, phép đối xứng tâm O biến đường thẳng AB thành đường thẳng CD, biến đường thẳng AC thành đường thẳng CA (chính nó).
Bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc ứng dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có. Thông thường, đề bài sẽ yêu cầu bạn giải một phương trình, bất phương trình, hoặc tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số.
Để giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu giải phương trình: x^2 - 4x + 3 = 0
Để đạt được kết quả tốt nhất khi giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều, bạn cần lưu ý những điều sau:
Việc giải bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều không chỉ giúp bạn hoàn thành bài tập về nhà mà còn có nhiều ứng dụng thực tế:
Bài 4 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tốt!