Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chương trình. Bài tập này thường yêu cầu vận dụng các công thức, định lý và phương pháp giải toán đã được trình bày trong chuyên đề.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Phép đối xứng tâm có là phép quay hay không? Vì sao?

Đề bài

Phép đối xứng tâm có là phép quay hay không? Vì sao?

Phương pháp giải - Xem chi tiết Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều 1

Dựa vào kiến thức:

- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({D_O}\). Điểm O được gọi là tâm đối xứng.

- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.

Lời giải chi tiết

Phép đối xứng tâm là phép quay.

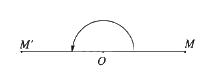
Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều 2

Thật vậy, cho điểm O, với mỗi điểm M, ta có M' là ảnh của điểm M qua phép đối xứng tâm O khi O là trung điểm của đoạn thẳng MM', suy ra \(OM{\rm{ }} = {\rm{ }}OM'\) và \(\widehat {MOM'} = 180^\circ \).

Khi đó góc lượng giác \(\;\left( {OM;{\rm{ }}OM'} \right)\) có số đo bằng (2k + 1)π và \(OM{\rm{ }} = {\rm{ }}OM'\)nên ta có phép quay tâm O, góc quay \(\left( {2k + 1} \right)\pi \) biến điểm M thành điểm M'.

Vậy phép đối xứng tâm O là phép quay \({Q_{(O,{\rm{ }}\left( {2k{\rm{ }} + {\rm{ }}1} \right)\pi )}}.\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng học toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều: Hướng dẫn chi tiết và đầy đủ

Bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và cách vẽ đồ thị hàm số.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định rõ hàm số cần xét, các điều kiện ràng buộc, và mục tiêu cần đạt được. Việc phân tích đề bài một cách cẩn thận sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.

Phương pháp giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Để giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều, học sinh có thể áp dụng các phương pháp sau:

Phương pháp xét dấu: Sử dụng phương pháp xét dấu để xác định khoảng đồng biến, nghịch biến của hàm số.
Phương pháp tìm cực trị: Tìm các điểm cực trị của hàm số bằng cách giải phương trình đạo hàm bằng 0.
Phương pháp vẽ đồ thị: Vẽ đồ thị hàm số dựa trên các thông tin đã thu thập được, bao gồm tập xác định, tập giá trị, tính đơn điệu, cực trị, và các điểm đặc biệt.
Phương pháp sử dụng máy tính bỏ túi: Sử dụng máy tính bỏ túi để tính toán các giá trị cần thiết và vẽ đồ thị hàm số một cách nhanh chóng và chính xác.

Lời giải chi tiết bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều

Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Cho hàm số y = x³ - 3x² + 2. Tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.)

Lời giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm cực trị: Giải phương trình y' = 0, ta được x = 0 và x = 2.
Xét dấu đạo hàm:
- Khi x < 0, y' > 0, hàm số đồng biến.
- Khi 0 < x < 2, y' < 0, hàm số nghịch biến.
- Khi x > 2, y' > 0, hàm số đồng biến.
Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số có cực đại tại x = 0, giá trị cực đại là y = 2, và có cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Ví dụ minh họa và bài tập tương tự

Để hiểu rõ hơn về cách giải bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều, học sinh có thể tham khảo các ví dụ minh họa sau:

(Ví dụ 1: Giải bài tập tương tự với hàm số khác)

(Ví dụ 2: Giải bài tập ứng dụng về hàm số)

Lưu ý khi giải bài tập về hàm số

Luôn kiểm tra lại kết quả sau khi giải bài.
Sử dụng máy tính bỏ túi để kiểm tra lại các phép tính.
Tham khảo các tài liệu học tập và bài giảng của giáo viên.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Tổng kết

Bài 2 trang 23 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về hàm số. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự một cách hiệu quả.