Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 5 của Chuyên đề học tập Toán 11 - Cánh diều, cụ thể là các trang 17, 18, 19 và 20.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
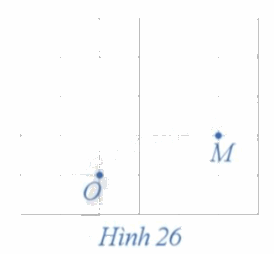
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
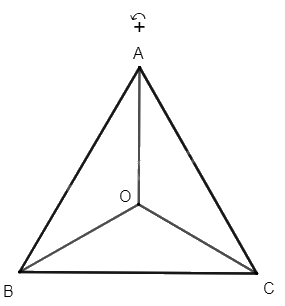
Ta có tam giác ABC đều có O là trọng tâm nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 120^\circ \) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\). Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
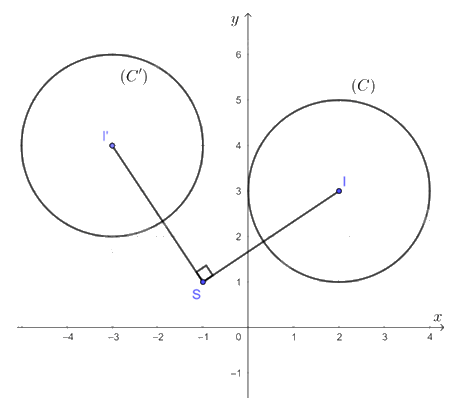
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
Phương pháp giải:
Tìm ảnh của tâm I qua phép quay bằng cách:
Phép quay tâm O, góc 900: Khi đó: \(\left\{ \begin{array}{l}x' = - y\\y' = x\end{array} \right.\)
Từ đó xác định ảnh của (C)
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
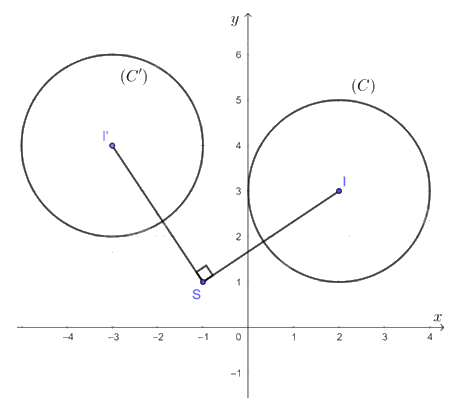
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải:
- Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90°
Lời giải chi tiết:
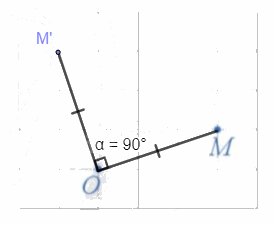
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
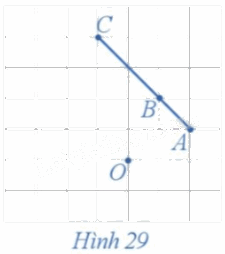
Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
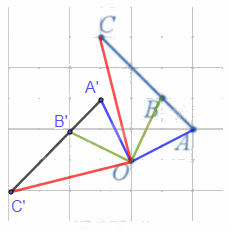
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
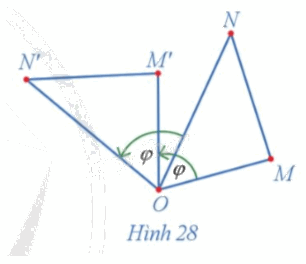
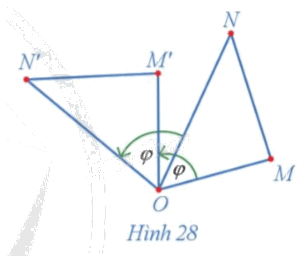
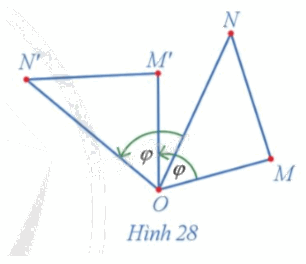
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
Phương pháp giải:
Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN.
Lời giải chi tiết:
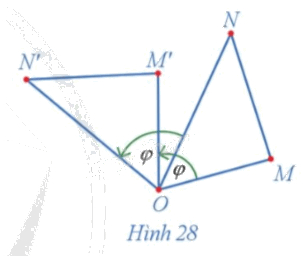
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay \(\varphi \) nên \(OM{\rm{ }} = {\rm{ }}OM',{\rm{ }}ON{\rm{ }} = {\rm{ }}ON'.\)
Ta có:
\(\begin{array}{l}\widehat {MON} + \widehat {NOM'} = \widehat {MOM'} = \varphi \\\widehat {NOM'} + \widehat {M'ON'} = \widehat {NON'} = \varphi \end{array}\)
Suy ra \(\widehat {MON} = \widehat {M'ON'}\)
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
\(\widehat {MON} = \widehat {M'ON'}\) cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ \(\Delta OM'N'{\rm{ }} = {\rm{ }}\Delta OMN\), suy ra M'N' = MN (hai cạnh tương ứng).
Trong mặt phẳng, cho điểm O cố định. Với mỗi điểm M (M khác O) trong mặt phẳng, hãy xác định điểm M' sao cho OM' = OM và góc lượng giác (OM, OM') = 90° (Hình 26).
Phương pháp giải:
- Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Xác định điểm M' thỏa mãn điều kiện: OM' = OM và góc lượng giác (OM, OM') = 90°
Lời giải chi tiết:
Cách xác định:
- Nối O với M;
- Qua O kẻ đường thẳng vuông góc với OM, trên đường thẳng, lấy điểm M' theo chiều dương sao cho OM' = OM.
Cho tam giác đều ABC có trọng tâm O. Xác định ảnh của các điểm A, B, C, qua phép quay tâm O với góc quay – 120°.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
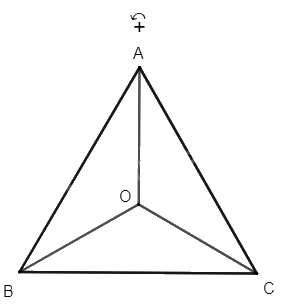
Ta có tam giác ABC đều có O là trọng tâm nên \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 120^\circ \) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC\). Vì phép quay với góc quay – 120° có chiều quay cùng chiều kim đồng hồ nên ảnh của các điểm A, B, C qua phép quay tâm O với góc quay – 120° lần lượt là các điểm C, A, B.
Trong Hình 28, cho các điểm M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay φ.
a) Hai tam giác OM'N' và OMN có bằng nhau hay không?
b) So sánh hai đoạn thẳng M'N' và MN.
Phương pháp giải:
Xét 2 tam giác OM'N' và OMN bằng nhau theo trường hợp c – g – c. Từ đó so sánh hai đoạn thẳng M'N' và MN.
Lời giải chi tiết:
a) Vì M', N' lần lượt là ảnh của các điểm M, N qua phép quay tâm O với góc quay \(\varphi \) nên \(OM{\rm{ }} = {\rm{ }}OM',{\rm{ }}ON{\rm{ }} = {\rm{ }}ON'.\)
Ta có:
\(\begin{array}{l}\widehat {MON} + \widehat {NOM'} = \widehat {MOM'} = \varphi \\\widehat {NOM'} + \widehat {M'ON'} = \widehat {NON'} = \varphi \end{array}\)
Suy ra \(\widehat {MON} = \widehat {M'ON'}\)
Xét hai tam giác OM'N' và OMN ta có:
OM = OM' (cmt)
\(\widehat {MON} = \widehat {M'ON'}\) cmt)
ON = ON' (cmt)
Do đó, hai tam giác OM'N' và OMN bằng nhau (c – g – c).
b) Từ \(\Delta OM'N'{\rm{ }} = {\rm{ }}\Delta OMN\), suy ra M'N' = MN (hai cạnh tương ứng).
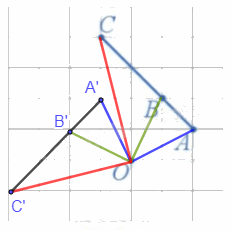
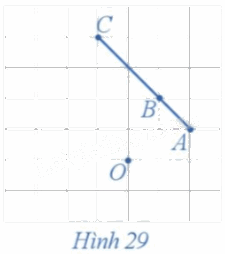
Xét phép quay tâm O với góc quay 90° (Hình 29).
a) Xác định các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay trên.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết:
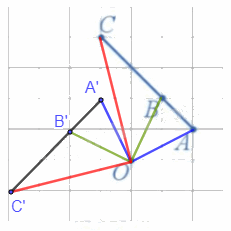
a) Các điểm A', B', C' lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép quay tâm O, góc quay 90° được xác định như hình vẽ trên.
b) Nhận thấy ba điểm A', B', C' thẳng hàng và B' nằm giữa A' và C'.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(2; 3) bán kính R = 2. Xác định ảnh của (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90°.
Phương pháp giải:
Tìm ảnh của tâm I qua phép quay bằng cách:
Phép quay tâm O, góc 900: Khi đó: \(\left\{ \begin{array}{l}x' = - y\\y' = x\end{array} \right.\)
Từ đó xác định ảnh của (C)
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Khi đó ta có I' là ảnh của I qua phép quay tâm S(– 1; 1) với góc quay φ = 90°. Suy ra I'(– 3; 4).
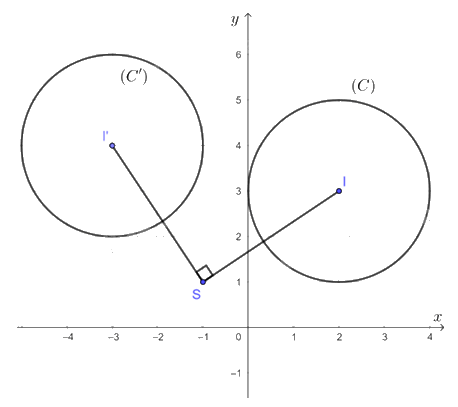
Vậy ảnh đường tròn (C) qua phép quay tâm S(– 1; 1) với góc quay φ = 90° là đường tròn (C') có tâm I'(– 3; 4), bán kính R' = 2.
Mục 5 của Chuyên đề học tập Toán 11 - Cánh Diều tập trung vào các kiến thức và kỹ năng liên quan đến đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong các kỳ thi.
Mục 5 bao gồm các nội dung chính sau:
Trang 17 tập trung vào việc ôn lại kiến thức về giới hạn và đạo hàm của hàm số tại một điểm. Các bài tập thường yêu cầu học sinh vận dụng định nghĩa để tính đạo hàm của các hàm số đơn giản.
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x2 tại x = 2.
Giải:
f'(2) = limh→0 (f(2+h) - f(2)) / h = limh→0 ((2+h)2 - 22) / h = limh→0 (4 + 4h + h2 - 4) / h = limh→0 (4h + h2) / h = limh→0 (4 + h) = 4.
Trang 18 giới thiệu về đạo hàm của hàm số và các quy tắc tính đạo hàm. Các bài tập yêu cầu học sinh áp dụng các quy tắc để tính đạo hàm của các hàm số phức tạp hơn.
Ví dụ 2: Tính đạo hàm của hàm số f(x) = 3x3 - 2x2 + 5x - 1.
Giải:
f'(x) = 9x2 - 4x + 5.
Trang 19 tập trung vào đạo hàm của các hàm số sơ cấp. Các bài tập yêu cầu học sinh nhớ và áp dụng các công thức đạo hàm của các hàm số lượng giác, hàm số mũ và hàm số logarit.
Ví dụ 3: Tính đạo hàm của hàm số f(x) = sin(x) + cos(x).
Giải:
f'(x) = cos(x) - sin(x).
Trang 20 đưa ra các bài tập ứng dụng của đạo hàm, như tìm cực trị của hàm số và khảo sát hàm số. Các bài tập này đòi hỏi học sinh phải kết hợp kiến thức về đạo hàm và các kỹ năng giải toán khác.
Ví dụ 4: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải:
f'(x) = 3x2 - 6x.
Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
f''(x) = 6x - 6.
f''(0) = -6 < 0, nên hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
f''(2) = 6 > 0, nên hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Hy vọng rằng với những giải thích chi tiết và ví dụ minh họa trên, bạn đã hiểu rõ hơn về cách giải các bài tập trong mục 5 trang 17, 18, 19, 20 Chuyên đề học tập Toán 11 - Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!