Bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hình 59 mô tả một viên gạch trang trí hình tam giác đều.
Đề bài
Hình 59 mô tả một viên gạch trang trí hình tam giác đều. Chứng minh rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.

Phương pháp giải - Xem chi tiết
- Phép biến hình F biến 2 điểm M, N bất kì thành 2 điểm M’, N’ sao cho \(M'N' = kMN\) với k là số thực dương cho trước, gọi là phép đồng dạng tỉ số k.
- Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
Gọi viên gạch trang trí là ABC, giao của các canh hoa màu đỏ với BC, CA, AB lần lượt là các điểm D, E, F, G là tâm của hình tam giác đều, khi đó G là tâm của các hình hoa (quan sát hình vẽ dưới đây).
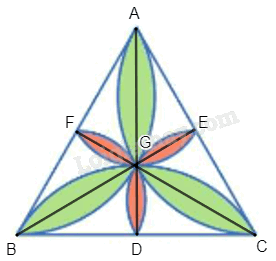
Qua phép quay tâm G, góc quay 120° hình cánh hoa màu xanh đỉnh A biến thành hình cánh hoa màu xanh đỉnh B, hình cánh hoa màu xanh đỉnh B biến thành hình cánh hoa màu xanh đỉnh C, hình cánh hoa màu đỏ đỉnh F biến thành hình cánh hoa màu đỏ đỉnh D, hình cánh hoa màu đỏ đỉnh D biến thành hình cánh hoa màu đỏ đỉnh E. Do đó, các hình cánh hoa màu xanh đồng dạng với nhau theo tỉ số 1 và các hình cánh hoa màu đỏ đồng dạng với nhau theo tỉ số 1 (phép dời hình là phép đồng dạng tỉ số 1).
Do đó, \(GA{\rm{ }} = {\rm{ }}GB{\rm{ }} = {\rm{ }}GC\) và \(GD{\rm{ }} = {\rm{ }}GE{\rm{ }} = {\rm{ }}GF\).
Ta có G là tâm của hình tam giác đều ABC nên G cũng là trọng tâm của tam giác ABC và D, E, F lần lượt là trung điểm của BC, CA, AB. Khi đó ta có: \(\overrightarrow {GD} = - \frac{1}{2}\overrightarrow {GA} ,\,\,\overrightarrow {GE} = - \frac{1}{2}\overrightarrow {GB} \) và \(\,\overrightarrow {GF} = - \frac{1}{2}\overrightarrow {GC} \) . Do đó, D, E, F lần lượt là ảnh của A, B, C qua phép vị tự tâm G, tỉ số \( - \frac{1}{2}\). Như vậy, khi ta lấy mỗi điểm bất kì trên hình hoa ba cánh màu xanh thì qua phép vị tự tâm G, tỉ số, điểm đó đều biến thành một điểm tương ứng trên hình hoa ba cánh màu đỏ. Vậy có phép đồng dạng biến hình hoa ba cánh màu xanh thành hình hoa ba cánh màu đỏ. Do đó, rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.
Bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học về đạo hàm, một trong những khái niệm nền tảng của giải tích. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán liên quan đến sự biến thiên của hàm số.
Bài 12 thường xoay quanh việc tìm đạo hàm của các hàm số phức tạp hơn, hoặc ứng dụng đạo hàm để giải các bài toán về cực trị, khoảng đơn điệu của hàm số. Để giải bài tập này hiệu quả, học sinh cần:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 12. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và phân tích các bài tập tương tự, chúng ta có thể đưa ra một ví dụ minh họa về cách giải bài tập đạo hàm:
Bài toán: Tìm đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
Ngoài việc tính đạo hàm trực tiếp, bài 12 trang 33 có thể xuất hiện các dạng bài tập sau:
Để giải các dạng bài tập này, học sinh cần nắm vững các kiến thức về đạo hàm và luyện tập thường xuyên.
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, học sinh nên:
Bài 12 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững lý thuyết, luyện tập thường xuyên và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 11.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và những hướng dẫn trên sẽ giúp các em học sinh học tập hiệu quả hơn. Chúc các em thành công!