Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chuyên đề học tập của Cánh Diều tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục 1, trang 26, 27, 28, 29, 30, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những giải pháp học tập hiệu quả nhất.
Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (Hình 47).
Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {OA'} ,\,\overrightarrow {OB'} \) lần lượt theo các vectơ \(\overrightarrow {OA} ,\,\overrightarrow {OB} \).
b) Biểu diễn các vectơ \(\overrightarrow {A'B'} \) theo vectơ \(\overrightarrow {AB} \). Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A'B' và AB.
Phương pháp giải:
Sử dụng quy tắc hiệu và tính chất \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'} = k\overrightarrow {OA} \).
Lời giải chi tiết:
a) Vì \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right)\) nên \(\overrightarrow {OA'} = k\overrightarrow {OA} ,\,\,\overrightarrow {OB'} = k\overrightarrow {OB} \)
b) Ta có: \(\overrightarrow {A'B'} = \overrightarrow {OB'} - \overrightarrow {OA'} = k\overrightarrow {OB} - k\overrightarrow {OA} = k\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) = k\overrightarrow {AB} \) (theo quy tắc hiệu).
Vậy \(\overrightarrow {A'B'} = k\overrightarrow {AB} \), từ đó suy ra \(A'B' = \left| k \right|AB.\)
Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {B'A'} ,\,\overrightarrow {B'C'} \) lần lượt theo các vectơ \(\overrightarrow {BA} ,\,\overrightarrow {BC} \).
b) Hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) có ngược hướng không?
c) Hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {B'C'} \) có ngược hướng không? Từ đó, nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Làm tương tự Hoạt động 2, sử dụng quy tắc hiệu và tính chất \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'} = k\overrightarrow {OA} \).
Lời giải chi tiết:
a) Vì \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).\) nên \(\overrightarrow {B'A'} = k\overrightarrow {BA} \) và \(\overrightarrow {B'C'} = k\overrightarrow {BC} \).
b) Vì A, B, C thẳng hàng và B nằm giữa A và C nên hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \)ngược hướng với nhau.
c) +) Với k > 0, ta có:
\(\overrightarrow {B'A'} = k\overrightarrow {BA} \) nên hai vectơ \(\overrightarrow {B'A'} ,\,\overrightarrow {BA} \) cùng hướng với nhau.
\(\overrightarrow {B'C'} = k\overrightarrow {BC} \) nên hai vectơ \(\overrightarrow {B'C'} ,\,\overrightarrow {BC} \) cùng hướng với nhau.
Mà hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) ngược hướng với nhau nên hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {B'C'} \) ngược hướng với nhau.
+) Với k < 0, ta có:
\(\overrightarrow {B'A'} = k\overrightarrow {BA} \) nên hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {BA} \) ngược hướng với nhau.
\(\overrightarrow {B'C'} = k\overrightarrow {BC} \) nên hai vectơ \(\overrightarrow {B'C'} \) và \(\overrightarrow {BC} \) ngược hướng với nhau.
Mà hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) ngược hướng với nhau nên hai vectơ và ngược hướng với nhau.
Từ đó suy ra với k ≠ 0 thì hai vectơ null và \(\overrightarrow {B'C'} \) ngược hướng với nhau.
Do đó, ba điểm A', B', C' thẳng hàng và B' nằm giữa hai điểm A' và C'.
Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số \(k = \frac{1}{2}\).
Phương pháp giải:
Tìm ảnh của A, B, C qua phép vị tự tâm O, tỉ số \(k = \frac{1}{2}\) là A’B’C’. Khi đó ảnh của tam giác ABC qua phép vị tự chính là tam giác A’B’C’.
Lời giải chi tiết:
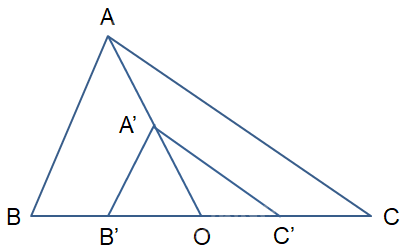
Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép vị tự tâm O tỉ số \(k = \frac{1}{2}\). Khi đó ta có:
\(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ;\,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ;\,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \). Do đó, các điểm A', B', C' lần lượt là trung điểm của OA, OB, OC.
Vậy ảnh của tam giác ABC trong phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) là tam giác A'B'C' với A', B', C' lần lượt là trung điểm của OA, OB, OC.
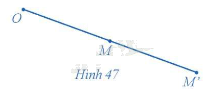
Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (Hình 47).
Phương pháp giải:
Quan sát hình 47, xác định M’ sao cho độ dài OM' = 2OM, và \(\overrightarrow {OM} ;\,\overrightarrow {OM'} \) cùng hướng.
Lời giải chi tiết:
Cách xác định:
- Lấy điểm O và điểm M bất kì;
- Trên tia OM, lấy điểm M' sao cho OM' = 2OM.
Khi đó ta có \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (tham khảo Hình 47).
Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số \(k = - \frac{1}{2}\).
Phương pháp giải:
Tìm ảnh của tâm O qua phép vị tự và \(R' = \;\left| k \right|R\)
Lời giải chi tiết:
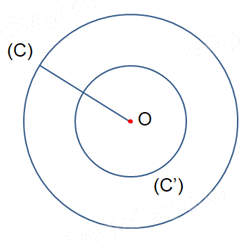
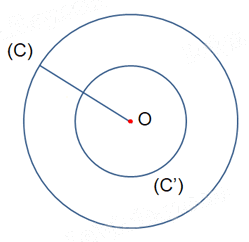
Qua phép vị tự tâm O tỉ số \(k = - \frac{1}{2}\) thì điểm O biến thành chính nó. Do đó, ảnh của đường tròn (C) là đường tròn (C') có tâm O và bán kính \(R' = \;\left| { - \frac{1}{2}} \right|R = \frac{1}{2}R\).
Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (Hình 47).
Phương pháp giải:
Quan sát hình 47, xác định M’ sao cho độ dài OM' = 2OM, và \(\overrightarrow {OM} ;\,\overrightarrow {OM'} \) cùng hướng.
Lời giải chi tiết:
Cách xác định:
- Lấy điểm O và điểm M bất kì;
- Trên tia OM, lấy điểm M' sao cho OM' = 2OM.
Khi đó ta có \(\overrightarrow {OM'} = 2\overrightarrow {OM} \) (tham khảo Hình 47).
Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số \(k = \frac{1}{2}\).
Phương pháp giải:
Tìm ảnh của A, B, C qua phép vị tự tâm O, tỉ số \(k = \frac{1}{2}\) là A’B’C’. Khi đó ảnh của tam giác ABC qua phép vị tự chính là tam giác A’B’C’.
Lời giải chi tiết:
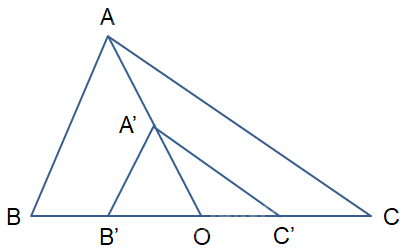
Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép vị tự tâm O tỉ số \(k = \frac{1}{2}\). Khi đó ta có:
\(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ;\,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ;\,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \). Do đó, các điểm A', B', C' lần lượt là trung điểm của OA, OB, OC.
Vậy ảnh của tam giác ABC trong phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) là tam giác A'B'C' với A', B', C' lần lượt là trung điểm của OA, OB, OC.
Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {OA'} ,\,\overrightarrow {OB'} \) lần lượt theo các vectơ \(\overrightarrow {OA} ,\,\overrightarrow {OB} \).
b) Biểu diễn các vectơ \(\overrightarrow {A'B'} \) theo vectơ \(\overrightarrow {AB} \). Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A'B' và AB.
Phương pháp giải:
Sử dụng quy tắc hiệu và tính chất \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'} = k\overrightarrow {OA} \).
Lời giải chi tiết:
a) Vì \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right)\) nên \(\overrightarrow {OA'} = k\overrightarrow {OA} ,\,\,\overrightarrow {OB'} = k\overrightarrow {OB} \)
b) Ta có: \(\overrightarrow {A'B'} = \overrightarrow {OB'} - \overrightarrow {OA'} = k\overrightarrow {OB} - k\overrightarrow {OA} = k\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) = k\overrightarrow {AB} \) (theo quy tắc hiệu).
Vậy \(\overrightarrow {A'B'} = k\overrightarrow {AB} \), từ đó suy ra \(A'B' = \left| k \right|AB.\)
Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).\)
a) Biểu diễn các vectơ \(\overrightarrow {B'A'} ,\,\overrightarrow {B'C'} \) lần lượt theo các vectơ \(\overrightarrow {BA} ,\,\overrightarrow {BC} \).
b) Hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) có ngược hướng không?
c) Hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {B'C'} \) có ngược hướng không? Từ đó, nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Làm tương tự Hoạt động 2, sử dụng quy tắc hiệu và tính chất \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right) \Rightarrow \overrightarrow {OA'} = k\overrightarrow {OA} \).
Lời giải chi tiết:
a) Vì \(A' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right),{\rm{ }}B' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right),{\rm{ }}C' = {V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right).\) nên \(\overrightarrow {B'A'} = k\overrightarrow {BA} \) và \(\overrightarrow {B'C'} = k\overrightarrow {BC} \).
b) Vì A, B, C thẳng hàng và B nằm giữa A và C nên hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \)ngược hướng với nhau.
c) +) Với k > 0, ta có:
\(\overrightarrow {B'A'} = k\overrightarrow {BA} \) nên hai vectơ \(\overrightarrow {B'A'} ,\,\overrightarrow {BA} \) cùng hướng với nhau.
\(\overrightarrow {B'C'} = k\overrightarrow {BC} \) nên hai vectơ \(\overrightarrow {B'C'} ,\,\overrightarrow {BC} \) cùng hướng với nhau.
Mà hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) ngược hướng với nhau nên hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {B'C'} \) ngược hướng với nhau.
+) Với k < 0, ta có:
\(\overrightarrow {B'A'} = k\overrightarrow {BA} \) nên hai vectơ \(\overrightarrow {B'A'} \) và \(\overrightarrow {BA} \) ngược hướng với nhau.
\(\overrightarrow {B'C'} = k\overrightarrow {BC} \) nên hai vectơ \(\overrightarrow {B'C'} \) và \(\overrightarrow {BC} \) ngược hướng với nhau.
Mà hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \) ngược hướng với nhau nên hai vectơ và ngược hướng với nhau.
Từ đó suy ra với k ≠ 0 thì hai vectơ null và \(\overrightarrow {B'C'} \) ngược hướng với nhau.
Do đó, ba điểm A', B', C' thẳng hàng và B' nằm giữa hai điểm A' và C'.
Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số \(k = - \frac{1}{2}\).
Phương pháp giải:
Tìm ảnh của tâm O qua phép vị tự và \(R' = \;\left| k \right|R\)
Lời giải chi tiết:
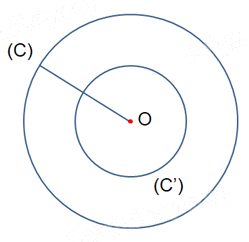
Qua phép vị tự tâm O tỉ số \(k = - \frac{1}{2}\) thì điểm O biến thành chính nó. Do đó, ảnh của đường tròn (C) là đường tròn (C') có tâm O và bán kính \(R' = \;\left| { - \frac{1}{2}} \right|R = \frac{1}{2}R\).
Mục 1 của Chuyên đề học tập Toán 11 Cánh Diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trang 26, 27, 28, 29, 30 là bước quan trọng để củng cố kiến thức và chuẩn bị cho các bài kiểm tra, thi cử.
Các bài tập trang 26 thường là những bài tập cơ bản, giúp học sinh làm quen với các khái niệm và định nghĩa mới. Lời giải chi tiết sẽ đi kèm với các bước thực hiện rõ ràng, giúp học sinh dễ dàng theo dõi và hiểu được cách giải.
Trang 27 thường chứa các bài tập áp dụng, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề cụ thể. Chúng tôi sẽ cung cấp các lời giải chi tiết, kèm theo các phân tích và giải thích để giúp học sinh hiểu rõ hơn về cách tiếp cận bài toán.
Các bài tập trang 28 có thể phức tạp hơn, đòi hỏi học sinh phải kết hợp nhiều kiến thức và kỹ năng khác nhau. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh tự tin giải quyết các bài toán tương tự.
Trang 29 thường chứa các bài tập nâng cao, dành cho những học sinh có khả năng học tập tốt. Chúng tôi sẽ cung cấp các lời giải chi tiết, kèm theo các gợi ý và phương pháp giải khác nhau để giúp học sinh khám phá và phát triển khả năng tư duy.
Các bài tập trang 30 thường là các bài tập tổng hợp, yêu cầu học sinh vận dụng tất cả các kiến thức và kỹ năng đã học trong mục 1. Lời giải sẽ được trình bày một cách đầy đủ và chính xác, giúp học sinh tự tin kiểm tra lại kiến thức của mình.
Kiến thức được học trong mục 1 của Chuyên đề học tập Toán 11 Cánh Diều có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, hóa học, kinh tế và kỹ thuật. Việc nắm vững kiến thức này sẽ giúp bạn có lợi thế trong học tập và công việc sau này.
| Công thức | Mô tả |
|---|---|
| Công thức A | Giải thích về công thức A |
| Công thức B | Giải thích về công thức B |
Hy vọng rằng với những lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, các em sẽ học tập tốt môn Toán 11 Chuyên đề học tập Cánh Diều. Chúc các em thành công!