Chào mừng bạn đến với giaitoan.edu.vn! Tại đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 của Chuyên đề học tập Toán 11 - Cánh diều, cụ thể là các trang 50, 51, 52, 53, 54, 55, 56 và 57.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Cho mặt phẳng (P), điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu vuông góc trên mặt phẳng (P) của:
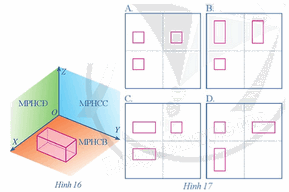
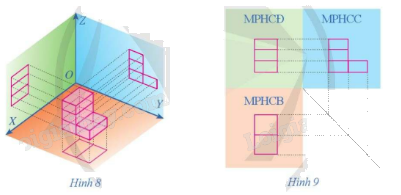
Khối hộp chữ nhật ở Hình 16 có các cạnh song song hoặc vuông góc với các tia OX, OY, OZ. Theo phương pháp góc chiếu thứ nhất, bản vẽ nào ở Hình 17 biểu diễn cho khối hộp chữ nhật đó?
Phương pháp giải:
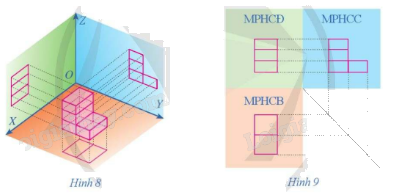
Phương pháp góc chiếu thứ nhất là phương pháp biểu diễn các hình chiếu bằng, hình chiếu xạnh, hình chiếu đứng của vật thể trên cùng một mặt phẳng (bản vẽ) theo thứ tự trong hình 9.
Lời giải chi tiết:
Theo phương pháp góc chiếu thứ nhất, bản vẽ D ở Hình 17 biểu diễn cho khối hộp chữ nhật đã cho ở Hình 16.
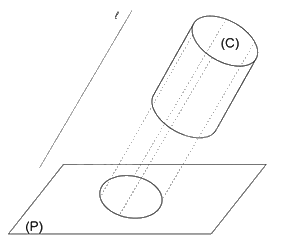
Cho hình trụ có đáy trên là đường tròn (C), đường thẳng ℓ song song với đường sinh của hình trụ, mặt phẳng (P) không song song với mặt đáy của hình trụ. Hãy xác định hình chiếu song song của đường tròn (C) trên mặt phẳng (P) theo phương ℓ.
Phương pháp giải:
Hình biểu diễn của một hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Lời giải chi tiết:
Lấy các điểm thuộc đường tròn đáy của hình trụ và xác định hình chiếu của các điểm đó trên mặt phẳng (P) theo phương ℓ. Khi đó ta được hình chiếu song song của đường tròn (C) trên mặt phẳng (P) theo phương ℓ như hình vẽ dưới đây.
Cho mặt phẳng (P) và đường thẳng ℓ cắt mặt phẳng (P). Cho điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu song song trên mặt phẳng (P) theo phương ℓ của:
a) Điểm M;
b) Đoạn thẳng AB;
c) Đường thẳng a.
Phương pháp giải:
Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) sao cho MM’ song song hoặc trùng với \(l\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
Lời giải chi tiết:
a)
+) TH1: Điểm M thuộc mặt phẳng (P) thì hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Điểm M thuộc đường thẳng ℓ (M không thuộc (P)) thì hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
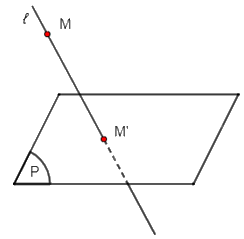
+) TH3: Điểm M nằm ngoài mặt phẳng (P) và đường thẳng ℓ: Từ điểm M, kẻ đường thẳng song song với ℓ, đường thẳng này cắt mặt phẳng (P) tại M'. Vậy M' là hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ.
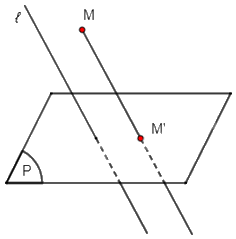
b)
+) TH1: Đoạn thẳng AB nằm trong mặt phẳng (P) thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Đoạn thẳng AB nằm trên đường thẳng ℓ thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
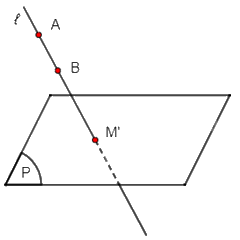
+) TH3: Đoạn thẳng AB song song với ℓ thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là giao điểm M' của đường thẳng AB với mặt phẳng (P).
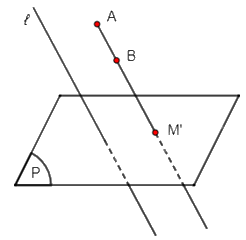
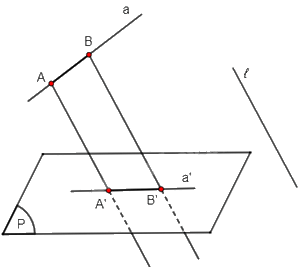
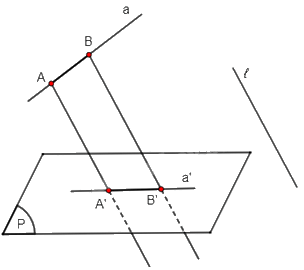
+) TH4: Đoạn thẳng AB thỏa mãn đường thẳng AB không song song hoặc trùng với ℓ và đoạn thẳng AB không nằm trong mặt phẳng (P).
Gọi A', B' lần lượt là hình chiếu song song của A, B trên mặt phẳng (P) theo phương ℓ.
Khi đó hình chiếu song song đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là đoạn thẳng A'B'.
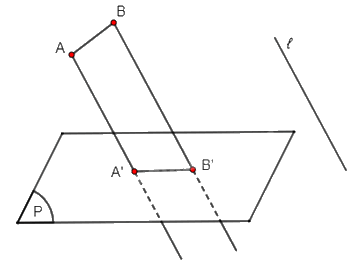
c)
+) TH1: Đường thẳng a nằm trong mặt phẳng (P) thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Đường thẳng a trùng với đường thẳng ℓ thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
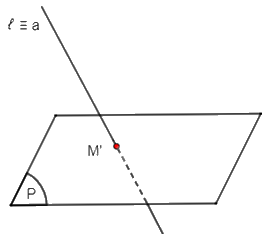
+) TH3: Đường thẳng a song song với ℓ thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là giao điểm M' của đường thẳng a với mặt phẳng (P).
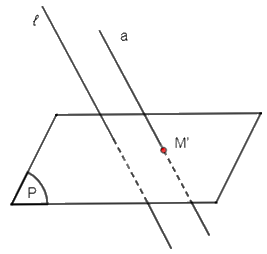
+) TH4: Đường thẳng a không song song hoặc trùng với ℓ và đường thẳng a không nằm trong mặt phẳng (P).
Lấy hai điểm A, B bất kì trên đường thẳng a. Gọi A', B' lần lượt là hình chiếu song song của A, B trên mặt phẳng (P) theo phương ℓ.
Khi đó hình chiếu song song đường thẳng a trên mặt phẳng (P) theo phương ℓ là đường thẳng a' đi qua hai điểm A', B'.
Cho mặt phẳng (P), điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu vuông góc trên mặt phẳng (P) của:
a) Điểm M;
b) Đoạn thẳng AB;
c) Đường thẳng a.
Phương pháp giải:
Để tìm hình chiếu vuông góc của một điểm A nằm ngoài mặt phẳng (P), từ điểm đó hạ đường thẳng vuông góc với mặt phẳng (P) tại H. Khi đó, H chính là hình chiếu vuông góc của A lên mặt phẳng (P).
Lời giải chi tiết:
a)
+) TH1: Điểm M thuộc mặt phẳng (P) thì hình chiếu vuông góc của M lên mặt phẳng (P) là chính nó.
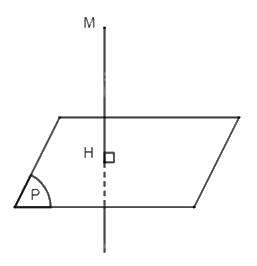
+) TH2: Điểm M không thuộc mặt phẳng (P).
Từ M kẻ đường thẳng vuông góc với mặt phẳng (P), đường thẳng này cắt mặt phẳng (P) tại H. Vậy H là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
b) Tùy theo vị trí của đoạn thẳng so với mặt phẳng hình chiếu, ta có 3 trường hợp:
+) TH1: Đoạn thẳng xiên với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng không song song và có độ dài không bằng nó (A'B' < AB).
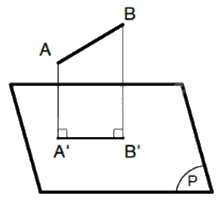
+) TH2: Đoạn thẳng song song với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng song song và có độ dài bằng nó (A'B' = AB).
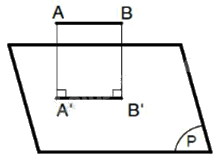
+) TH3: Đoạn thẳng vuông góc với mặt phẳng hình chiếu: hình chiếu của nó là một điểm (A' ≡ B').
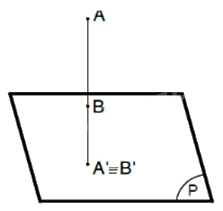
c)
+) TH1: Đường thẳng a nằm trong mặt phẳng (P) thì hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là chính nó.
+) TH2: Đường thẳng a cắt mặt phẳng (P).
Gọi M là giao điểm của đường thẳng a và mặt phẳng (P). Lấy điểm B khác M thuộc đường thẳng a, xác định hình chiếu vuông góc H của B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a lên mặt phẳng (P) là đường thẳng đi qua hai điểm M và H.
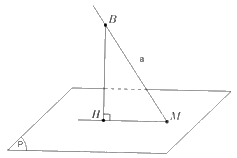
Tổng quát:
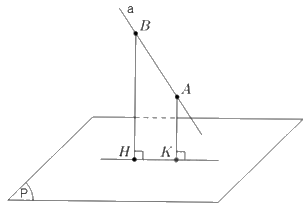
+) TH3: Đường thẳng a song song với mặt phẳng (P).
Lấy hai điểm A, B khác nhau trên đường thẳng a, xác định hình chiếu vuông góc A', B' lần lượt của A và B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là đường thẳng A'B' (A'B' // a).
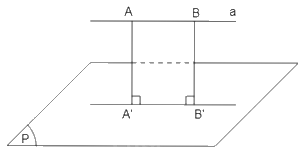
+) TH4: Đường thẳng a vuông góc với mặt phẳng (P).
Khi đó hình chiếu vuông của đường thẳng a trên mặt phẳng (P) là giao điểm M của a và (P).
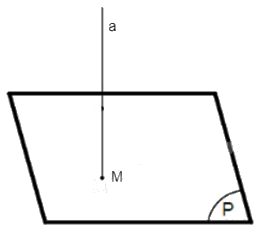
Cho mặt phẳng (P), điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu vuông góc trên mặt phẳng (P) của:
a) Điểm M;
b) Đoạn thẳng AB;
c) Đường thẳng a.
Phương pháp giải:
Để tìm hình chiếu vuông góc của một điểm A nằm ngoài mặt phẳng (P), từ điểm đó hạ đường thẳng vuông góc với mặt phẳng (P) tại H. Khi đó, H chính là hình chiếu vuông góc của A lên mặt phẳng (P).
Lời giải chi tiết:
a)
+) TH1: Điểm M thuộc mặt phẳng (P) thì hình chiếu vuông góc của M lên mặt phẳng (P) là chính nó.
+) TH2: Điểm M không thuộc mặt phẳng (P).
Từ M kẻ đường thẳng vuông góc với mặt phẳng (P), đường thẳng này cắt mặt phẳng (P) tại H. Vậy H là hình chiếu vuông góc của điểm M lên mặt phẳng (P).
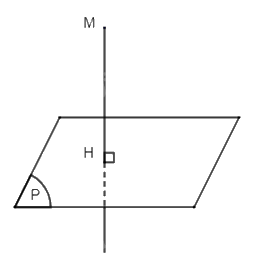
b) Tùy theo vị trí của đoạn thẳng so với mặt phẳng hình chiếu, ta có 3 trường hợp:
+) TH1: Đoạn thẳng xiên với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng không song song và có độ dài không bằng nó (A'B' < AB).
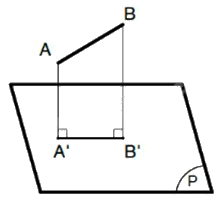
+) TH2: Đoạn thẳng song song với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng song song và có độ dài bằng nó (A'B' = AB).
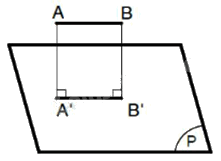
+) TH3: Đoạn thẳng vuông góc với mặt phẳng hình chiếu: hình chiếu của nó là một điểm (A' ≡ B').
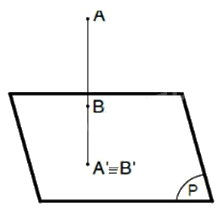
c)
+) TH1: Đường thẳng a nằm trong mặt phẳng (P) thì hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là chính nó.
+) TH2: Đường thẳng a cắt mặt phẳng (P).
Gọi M là giao điểm của đường thẳng a và mặt phẳng (P). Lấy điểm B khác M thuộc đường thẳng a, xác định hình chiếu vuông góc H của B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a lên mặt phẳng (P) là đường thẳng đi qua hai điểm M và H.
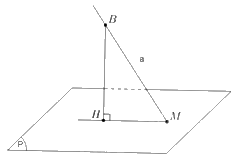
Tổng quát:
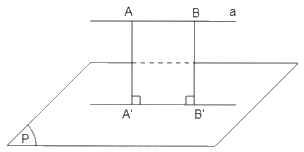
+) TH3: Đường thẳng a song song với mặt phẳng (P).
Lấy hai điểm A, B khác nhau trên đường thẳng a, xác định hình chiếu vuông góc A', B' lần lượt của A và B trên mặt phẳng (P). Khi đó hình chiếu vuông góc của đường thẳng a trên mặt phẳng (P) là đường thẳng A'B' (A'B' // a).
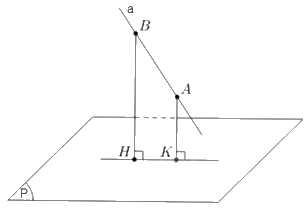
+) TH4: Đường thẳng a vuông góc với mặt phẳng (P).
Khi đó hình chiếu vuông của đường thẳng a trên mặt phẳng (P) là giao điểm M của a và (P).
Khối hộp chữ nhật ở Hình 16 có các cạnh song song hoặc vuông góc với các tia OX, OY, OZ. Theo phương pháp góc chiếu thứ nhất, bản vẽ nào ở Hình 17 biểu diễn cho khối hộp chữ nhật đó?
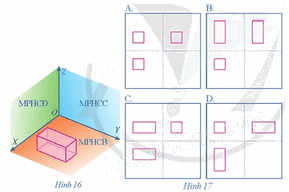
Phương pháp giải:
Phương pháp góc chiếu thứ nhất là phương pháp biểu diễn các hình chiếu bằng, hình chiếu xạnh, hình chiếu đứng của vật thể trên cùng một mặt phẳng (bản vẽ) theo thứ tự trong hình 9.
Lời giải chi tiết:
Theo phương pháp góc chiếu thứ nhất, bản vẽ D ở Hình 17 biểu diễn cho khối hộp chữ nhật đã cho ở Hình 16.
Cho mặt phẳng (P) và đường thẳng ℓ cắt mặt phẳng (P). Cho điểm M, đoạn thẳng AB và đường thẳng a. Xác định hình chiếu song song trên mặt phẳng (P) theo phương ℓ của:
a) Điểm M;
b) Đoạn thẳng AB;
c) Đường thẳng a.
Phương pháp giải:
Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) sao cho MM’ song song hoặc trùng với \(l\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
Lời giải chi tiết:
a)
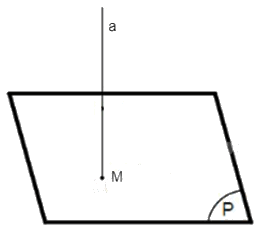
+) TH1: Điểm M thuộc mặt phẳng (P) thì hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Điểm M thuộc đường thẳng ℓ (M không thuộc (P)) thì hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
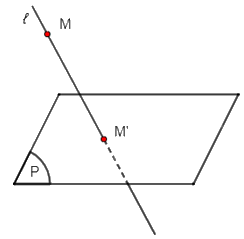
+) TH3: Điểm M nằm ngoài mặt phẳng (P) và đường thẳng ℓ: Từ điểm M, kẻ đường thẳng song song với ℓ, đường thẳng này cắt mặt phẳng (P) tại M'. Vậy M' là hình chiếu song song của điểm M trên mặt phẳng (P) theo phương ℓ.
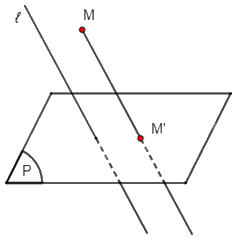
b)
+) TH1: Đoạn thẳng AB nằm trong mặt phẳng (P) thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Đoạn thẳng AB nằm trên đường thẳng ℓ thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
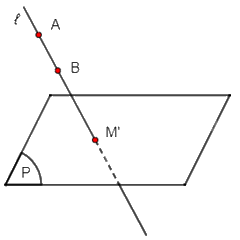
+) TH3: Đoạn thẳng AB song song với ℓ thì hình chiếu song song của đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là giao điểm M' của đường thẳng AB với mặt phẳng (P).
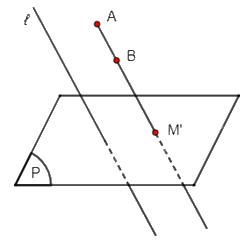
+) TH4: Đoạn thẳng AB thỏa mãn đường thẳng AB không song song hoặc trùng với ℓ và đoạn thẳng AB không nằm trong mặt phẳng (P).
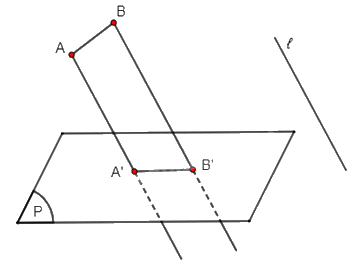
Gọi A', B' lần lượt là hình chiếu song song của A, B trên mặt phẳng (P) theo phương ℓ.
Khi đó hình chiếu song song đoạn thẳng AB trên mặt phẳng (P) theo phương ℓ là đoạn thẳng A'B'.
c)
+) TH1: Đường thẳng a nằm trong mặt phẳng (P) thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là chính nó.
+) TH2: Đường thẳng a trùng với đường thẳng ℓ thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là giao điểm M' của ℓ và (P).
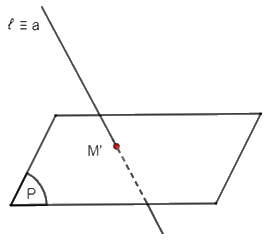
+) TH3: Đường thẳng a song song với ℓ thì hình chiếu song song của đường thẳng a trên mặt phẳng (P) theo phương ℓ là giao điểm M' của đường thẳng a với mặt phẳng (P).
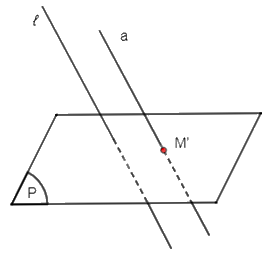
+) TH4: Đường thẳng a không song song hoặc trùng với ℓ và đường thẳng a không nằm trong mặt phẳng (P).
Lấy hai điểm A, B bất kì trên đường thẳng a. Gọi A', B' lần lượt là hình chiếu song song của A, B trên mặt phẳng (P) theo phương ℓ.
Khi đó hình chiếu song song đường thẳng a trên mặt phẳng (P) theo phương ℓ là đường thẳng a' đi qua hai điểm A', B'.
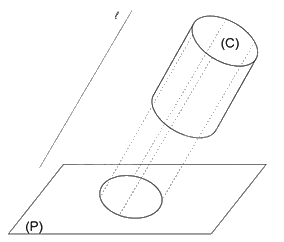
Cho hình trụ có đáy trên là đường tròn (C), đường thẳng ℓ song song với đường sinh của hình trụ, mặt phẳng (P) không song song với mặt đáy của hình trụ. Hãy xác định hình chiếu song song của đường tròn (C) trên mặt phẳng (P) theo phương ℓ.
Phương pháp giải:
Hình biểu diễn của một hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Lời giải chi tiết:
Lấy các điểm thuộc đường tròn đáy của hình trụ và xác định hình chiếu của các điểm đó trên mặt phẳng (P) theo phương ℓ. Khi đó ta được hình chiếu song song của đường tròn (C) trên mặt phẳng (P) theo phương ℓ như hình vẽ dưới đây.
Mục 1 của Chuyên đề học tập Toán 11 - Cánh diều thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trong mục này không chỉ giúp củng cố kiến thức mà còn rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Để hiểu rõ hơn về Mục 1, chúng ta cần xác định nội dung chính mà sách Cánh Diều tập trung vào. Thông thường, đây có thể là:
Dưới đây là phần giải chi tiết các bài tập từ trang 50 đến trang 57. Lưu ý rằng nội dung cụ thể của từng bài tập sẽ phụ thuộc vào phiên bản sách Cánh Diều mà bạn đang sử dụng. Chúng tôi sẽ cung cấp lời giải cho một số bài tập minh họa:
Đề bài: (Giả định một bài tập cụ thể về hàm số)
Lời giải:
Đề bài: (Giả định một bài tập cụ thể về phương trình)
Lời giải:
Sử dụng các phương pháp giải phương trình đã học, ta có thể tìm ra nghiệm của phương trình như sau:
Để giải các bài tập Toán 11 Cánh Diều một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Việc giải bài tập Toán 11 đóng vai trò quan trọng trong việc chuẩn bị cho kỳ thi THPT Quốc gia và các kỳ thi đại học. Toán 11 là nền tảng kiến thức quan trọng cho các môn học khác như Vật lý, Hóa học, Kinh tế. Do đó, việc nắm vững kiến thức và kỹ năng giải toán là rất cần thiết.
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc học tập môn Toán 11 - Cánh diều. Chúc bạn học tốt và đạt kết quả cao!