Chào mừng các em học sinh đến với lời giải chi tiết bài 11 trang 25 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
Đề bài
Hình 44 mô tả một viên gạch trang trí hình tam giác đều. Xác định phép quay biến:
a) Cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.
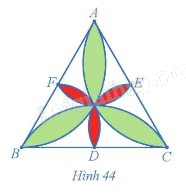
Phương pháp giải - Xem chi tiết
Xác định tâm và góc quay:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Lời giải chi tiết
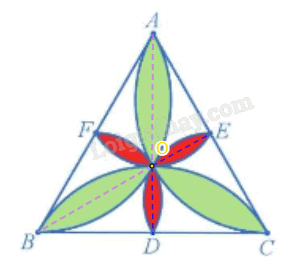
a) Đặt điểm O là tâm của các cánh hoa như hình vẽ. Do tam giác ABC là tam giác đều nên OA = OB và \(\widehat {AOB} = 120^\circ \). Do đó, ta có phép quay tâm O với góc quay 120° biến điểm O thành điểm O và điểm A thành điểm B. Như vậy, phép quay tâm O với góc quay 120° biến cánh hoa màu xanh đỉnh A thành cánh hoa màu xanh đỉnh B.
b) Ta cũng có OE = OD và \(\widehat {EOD} = 120^\circ \) nên ta có phép quay tâm O với góc quay – 120° biến điểm O thành điểm O, biến điểm E thành điểm D. Như vậy, phép quay tâm O với góc quay – 120° biến cánh hoa màu đỏ đỉnh E thành cánh hoa màu đỏ đỉnh D.
Bài 11 trang 25 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập trong chuyên đề này là vô cùng quan trọng, không chỉ giúp các em đạt kết quả tốt trong các bài kiểm tra, mà còn là nền tảng vững chắc cho việc học tập các kiến thức nâng cao hơn ở các lớp trên.
Bài 11 trang 25 Chuyên đề học tập Toán 11 Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 11 trang 25 Chuyên đề học tập Toán 11 Cánh diều, chúng ta sẽ đi vào giải chi tiết từng dạng bài tập:
Để xác định tập xác định của hàm số, ta cần tìm các giá trị của x sao cho biểu thức của hàm số có nghĩa. Ví dụ, nếu hàm số có chứa mẫu số, ta cần đảm bảo mẫu số khác 0. Nếu hàm số có chứa căn bậc chẵn, ta cần đảm bảo biểu thức dưới dấu căn lớn hơn hoặc bằng 0.
Để tìm tập giá trị của hàm số, ta cần tìm các giá trị của y mà hàm số có thể đạt được. Có nhiều phương pháp để tìm tập giá trị, như sử dụng đạo hàm, biến đổi tương đương, hoặc vẽ đồ thị hàm số.
Để xét tính đơn điệu của hàm số, ta cần tính đạo hàm của hàm số và xét dấu của đạo hàm trên các khoảng xác định. Nếu đạo hàm dương trên một khoảng, hàm số đồng biến trên khoảng đó. Nếu đạo hàm âm trên một khoảng, hàm số nghịch biến trên khoảng đó.
Để vẽ đồ thị hàm số, ta cần xác định các điểm đặc biệt của đồ thị, như điểm cực trị, điểm uốn, giao điểm với các trục tọa độ. Sau đó, ta vẽ đồ thị bằng cách nối các điểm này lại với nhau.
Để giải phương trình, bất phương trình chứa hàm số, ta cần sử dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi tương đương. Đôi khi, ta cần sử dụng các phương pháp đặc biệt, như phương pháp đặt ẩn phụ, phương pháp đánh giá.
Để giải bài tập Toán 11 hiệu quả, các em nên:
Hy vọng rằng, với lời giải chi tiết và các hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn trong việc giải bài 11 trang 25 Chuyên đề học tập Toán 11 Cánh diều và đạt kết quả tốt trong môn Toán. Chúc các em học tập tốt!