Bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài.
Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực.
Đề bài
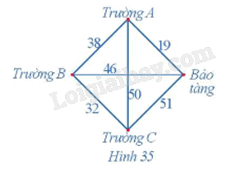
Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực. Người đó muốn đến từng trường và quay trở lại bảo tàng sau khi thăm cả ba trường. Thời gian di chuyển (đơn vị: phút) giữa các trường học và giữa bảo tàng với mỗi trường học được mô tả trong Hình 35.
Tìm chu trình xuất phát từ viện bảo tàng sao cho thời gian đi là ít nhất.
Phương pháp giải - Xem chi tiết
Bước 1. Chọn một đỉnh bắt đầu, ta gọi là đỉnh V.
Bước 2. Xuất phát từ đỉnh hiện hành, chọn cạnh có độ dài nhỏ nhất nối đến một trong các đỉnh chưa đến. Đánh dấu đỉnh cuối của cạnh vừa chọn.
Bước 3. Xuất phát từ đỉnh vừa đánh dấu, nếu còn đỉnh chưa đến thì quay lại bước 2.
Bước 4. Quay lại đỉnh V.
Lời giải chi tiết
Từ viện bảo tàng, thời gian di chuyển đến trường A là ngắn nhất: 19 phút.
Từ trường A, thời gian di chuyển đến trường B là ngắn nhất: 38 phút.
Từ trường B, thời gian di chuyển đến trường C là ngắn nhất: 32 phút.
Đến đây, không còn địa điểm nào chưa đi qua nên quay lại viện bảo tàng với thời gian di chuyển: 51 phút.
Do đó, chu trình xuất phát từ viện bảo tàng, qua trường A, trường B, trường C rồi quay lại viện bảo tàng có thời gian đi là ít nhất và thời gian đi là: 19 + 38 + 32 + 51 = 140 (phút).
Bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh tính đạo hàm của các hàm số lượng giác, hàm hợp, và áp dụng đạo hàm để giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều, chúng ta cần nắm vững các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Để tính đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp: y' = u' * v', trong đó u = 2x + 1 và v = sin(u).
Ta có: u' = 2 và v' = cos(u) = cos(2x + 1).
Vậy, y' = 2 * cos(2x + 1).
Tương tự như phần a, ta sử dụng quy tắc đạo hàm của hàm hợp. Đặt u = x^2 và v = cos(u).
Ta có: u' = 2x và v' = -sin(u) = -sin(x^2).
Vậy, y' = 2x * (-sin(x^2)) = -2x * sin(x^2).
Để tìm cực trị của hàm số, ta thực hiện các bước sau:
Ta có: y' = 3x^2 - 6x.
Giải phương trình y' = 0, ta được: 3x^2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2.
Ta có: y'' = 6x - 6.
Tại x = 0, y'' = -6 < 0, vậy x = 0 là điểm cực đại. Giá trị cực đại là y(0) = 2.
Tại x = 2, y'' = 6 > 0, vậy x = 2 là điểm cực tiểu. Giá trị cực tiểu là y(2) = -2.
Khi giải bài tập về đạo hàm, cần lưu ý các điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 5 trang 49 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và đạt kết quả tốt trong môn Toán.