Bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O.
Đề bài
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (Hình 58). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.
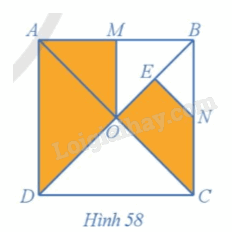
Phương pháp giải - Xem chi tiết
Phép biến hình F biến 2 điểm M, N bất kì thành 2 điểm M’, N’ sao cho \(M'N' = kMN\) với k là số thực dương cho trước, gọi là phép đồng dạng tỉ số k.
Lời giải chi tiết
Gọi G là trung điểm của BM.
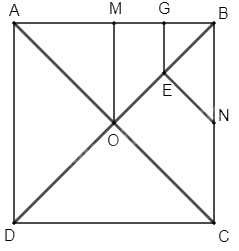
Khi đó, ta thấy Hình 58 và Hình 56 là hai hình giống nhau.
+) Theo kết quả Ví dụ 8 trang 32 thì hai hình BGEN và AMOD đồng dạng với nhau (1).
+) Theo kết quả Luyện tập 4 trang 32 thì hai hình OMGE và COEN đồng dạng với nhau hay hai hình MGEO và OENC đồng dạng với nhau (2).
+) Thực hiện phép đối xứng trục GE thì hình BGEN biến thành hình MGEO (3).
Do đó, hai hình BGEN và MGEO đồng dạng với nhau.
Từ (1), (2) và (3) suy ra hai hình AMOD và OENC đồng dạng với nhau.
Bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học về hàm số lượng giác. Bài tập này tập trung vào việc tìm tập xác định, tập giá trị, và các tính chất của hàm số lượng giác. Việc nắm vững kiến thức về hàm số lượng giác là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều, chúng ta cần thực hiện các bước sau:
Ví dụ, xét bài tập sau:
Tìm tập xác định của hàm số y = tan(2x + π/3).
Để tìm tập xác định của hàm số y = tan(2x + π/3), ta cần đảm bảo rằng cos(2x + π/3) ≠ 0. Điều này tương đương với:
2x + π/3 ≠ π/2 + kπ, với k là số nguyên.
Suy ra:
2x ≠ π/2 - π/3 + kπ = π/6 + kπ
x ≠ π/12 + kπ/2, với k là số nguyên.
Vậy, tập xác định của hàm số y = tan(2x + π/3) là:
D = {x | x ≠ π/12 + kπ/2, k ∈ Z}
Khi giải bài tập về hàm số lượng giác, các em học sinh cần lưu ý những điều sau:
Hàm số lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để củng cố kiến thức về hàm số lượng giác, các em học sinh có thể làm thêm các bài tập sau:
Bài 11 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hàm số lượng giác. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.