Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu sâu hơn về kiến thức đã học.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các tài liệu học tập chất lượng và lời giải bài tập chính xác.
Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A.
Đề bài
Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O1; R) thành đường tròn \(({O_2};{\rm{ }}2R).\)
Phương pháp giải - Xem chi tiết
- Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
- Phép vị tự biến đường tròn có bán kính R thành đường tròn có bán kính R' = |k|R và có tâm là ảnh của tâm.
Lời giải chi tiết
Hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A và đường tròn tâm O2 có bán kính gấp 2 lần đường tròn tâm O1.
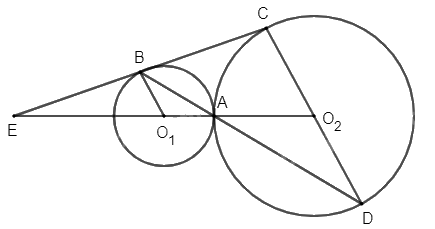
- Trên đường tròn \(({O_1};{\rm{ }}R)\) lấy điểm B bất kì.
- Trên đường tròn \(({O_2};{\rm{ }}2R)\) dựng đường kính CD // O1B.
- BC cắt O1O2 tại E.
+) Ta có: O1B // CO2 nên theo định lí Thales có \(\frac{{E{O_2}}}{{E{O_1}}} = \frac{{{O_2}C}}{{{O_1}B}} = \frac{{2R}}{R} = 2\).
Suy ra \(\overrightarrow {E{O_2}} = 2\overrightarrow {E{O_1}} \) nên ta có phép vị tự tâm E, tỉ số 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm E, tỉ số 2 biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}2R).\)
+) Nối B với D, ta chứng minh được BD cắt O1O2 tại điểm tiếp xúc A của hai đường tròn.
Ta có: \(\frac{{A{O_2}}}{{A{O_1}}} = \frac{{2R}}{R} = 2\) và A nằm giữa hai điểm O1 và O2 nên \(\overrightarrow {A{O_2}} = - 2\overrightarrow {A{O_1}} \). Do đó, ta có phép vị tự tâm A, tỉ số – 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm A, tỉ số – 2 biến đường tròn (O1; R) thành đường tròn \(({O_2};{\rm{ }}2R)\).
Vậy có 2 phép vị tự biến đường tròn \(({O_1};{\rm{ }}R)\) thành đường tròn \(({O_2};{\rm{ }}2R)\).
Bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 8 trang 33 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều một cách hiệu quả, học sinh cần:
Ví dụ: Tìm cực đại, cực tiểu của hàm số y = x3 - 3x2 + 2.
Giải:
Khi giải bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều, học sinh cần lưu ý:
Bài 8 trang 33 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.