Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chuyên đề học tập - Cánh diều. Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn, đặc biệt là với những chuyên đề phức tạp.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong học tập.
Trong mặt phẳng cho đường thẳng d.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng trục, sau đó viết phương trình đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2.
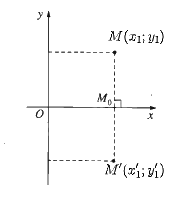
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
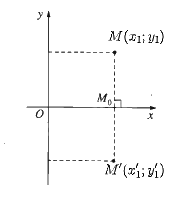
Do đó M'(x1; – y1) và N'(x2; – y2).
b) Ta có
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\M'N' = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {\left( { - {y_2}} \right) - \left( { - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
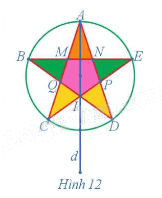
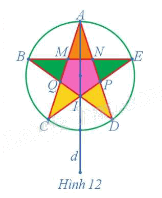
Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
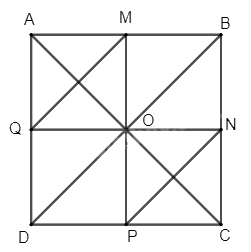
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.
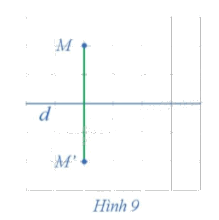
Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
Phương pháp giải:
Đường trung trực là đường đi qua trung điểm đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm.
Lời giải chi tiết:
Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM':
- Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H.
- Trên d', lấy điểm M' sao cho MH = M'H.
Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'.
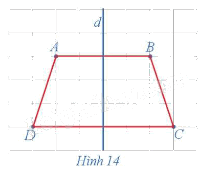
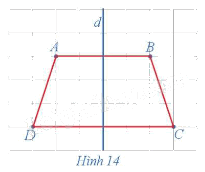
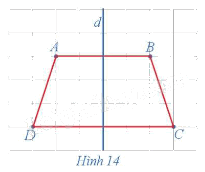
Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
Phương pháp giải:
Để tìm ảnh của (H) qua \(Đ_d\) ta tìm ảnh của các điểm thuococj (H) qua \(Đ_d\). Sau đó nối chúng với nhau.
Lời giải chi tiết:
Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD.
Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d.
Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
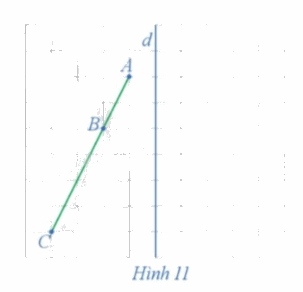
Xét phép đối xứng trục d (Hình 11)
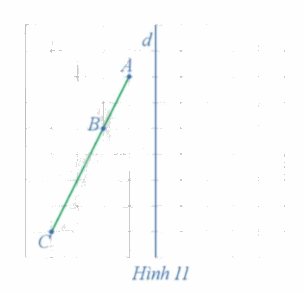
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Trong mặt phẳng cho đường thẳng d. Với mỗi điểm M trong mặt phẳng và M ∉ d, hãy xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM' (hay M' là điểm đối xứng với M qua đường thẳng d) (Hình 9).
Phương pháp giải:
Đường trung trực là đường đi qua trung điểm đoạn thẳng và vuông góc với đoạn thẳng tại trung điểm.
Lời giải chi tiết:
Cách xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM':
- Qua M kẻ đường thẳng d' vuông góc với đường thẳng d tại H.
- Trên d', lấy điểm M' sao cho MH = M'H.
Khi đó đường thẳng d vuông góc với MM' tại trung điểm H của MM' nên d là đường trung trực của đoạn thẳng MM'.
Cho hình vuông ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Xác định ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Gọi O là giao điểm hai đường chéo AC và BD của hình vuông ABCD.
Khi đó O là trung điểm của AC và BD. Ta chứng minh được O cũng là trung điểm của MP và QN. Lại có MP = QN = AB = BC = CD = DA nên ta suy ra OM = OQ = OP = ON = MA = MB = NB = NC = PC = PD = QD = QA.
+ Ta có AQ = AM và OQ = OM nên AO là đường trung trực của đoạn thẳng QM hay AC là đường trung trực của đoạn thẳng QM. Tương tự, ta chứng minh được AC là đường trung trực của đoạn thẳng PN.
Do đó, ta có phép đối xứng trục AC biến các điểm M, N, P, Q tương ứng thành các điểm Q, P, N, M.
Vậy ảnh của các điểm M, N, P, Q qua phép đối xứng trục AC lần lượt là các điểm Q, P, N, M.
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(x1; y1), N(x2; y2). Gọi M', N' lần lượt là ảnh của M và N qua phép đối xứng trục Ox.
a) Xác định tọa độ của hai điểm M' và N'.
b) Viết công thức tính độ dài hai đoạn thẳng MN và M'N', từ đó so sánh hai đoạn thẳng MN và M'N'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Với mỗi điểm M(x1; y1) ta có M'(x1'; y1') là ảnh của điểm M qua phép đối xứng trục Ox thì \(\left\{ {\begin{array}{*{20}{l}}{{x_1}' = {x_1}}\\{{y_1}' = - {y_1}}\end{array}} \right.\)
Do đó M'(x1; – y1) và N'(x2; – y2).
b) Ta có
\(\begin{array}{l}MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \\M'N' = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {\left( { - {y_2}} \right) - \left( { - {y_1}} \right)} \right)}^2}} \end{array}\)
Từ đó suy ra MN = M'N'.
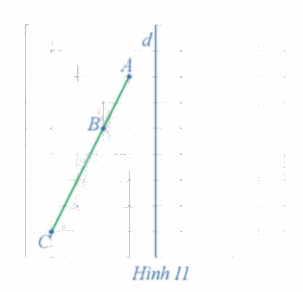
Xét phép đối xứng trục d (Hình 11)
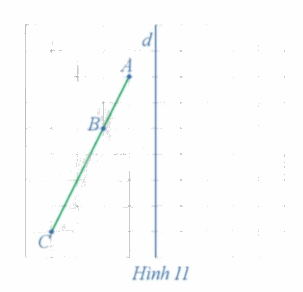
a) Xác định các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d.
b) Nêu mối quan hệ giữa ba điểm A', B', C'.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
a) Ta xác định được các điểm A', B', C' lần lượt là ảnh của các điểm thẳng hàng A, B, C qua phép đối xứng trục d như trên hình vẽ dưới đây.
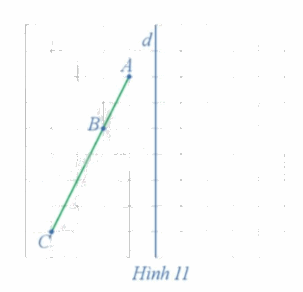
b) Từ hình vẽ ta thấy 3 điểm A', B', C' thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Xác định ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12.
Phương pháp giải:
Cho đường thẳng d, phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \(Đ_d\)
Lời giải chi tiết:
Ảnh của cánh sao màu vàng có các đỉnh D, I, P qua phép đối xứng trục d trong Hình 12 là cánh sao màu vàng có các đỉnh C, I, Q.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(3; 2), bán kính R = 2. Xác định ảnh của đường tròn (C) qua phép đối xứng trục Ox.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng trục, sau đó viết phương trình đường tròn (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng trục Ox là một đường tròn có bán kính R' = R = 2, gọi là (C').
Gọi I' là tâm của đường tròn (C'). Ta có I' là ảnh của I qua phép đối xứng trục Ox, suy ra I'(3; – 2). Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn (C') có tâm I'(3; – 2), bán kính R' = 2.
Trong mặt phẳng, cho hình thang cân ABCD, kí hiệu là ℋ. Gọi d là đường thẳng đi qua trung điểm hai cạnh đáy của hình thang cân đó (Hình 14).
Tìm ℋ' = Đd(ℋ).
Phương pháp giải:
Để tìm ảnh của (H) qua \(Đ_d\) ta tìm ảnh của các điểm thuococj (H) qua \(Đ_d\). Sau đó nối chúng với nhau.
Lời giải chi tiết:
Đường thẳng d đi qua trung điểm hai háy của hình thang cân ABCD nên đường thẳng d là đường trung trực của các đoạn thẳng AB và CD.
Khi đó, ta có phép đối xứng trục d biến các điểm A, B, C, D tương ứng thành các điểm B, A, D, C nên phép đối xứng trục d biến hình thang cân ABCD thành hình thang cân BADC hay hình thang cân ABCD là ảnh của chính nó qua phép đối xứng trục d.
Như vậy, ℋ ' ≡ ℋ hay phép đối xứng trục d biến hình ℋ thành chính nó.
Mục 3 của Chuyên đề học tập Toán 11 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 10, 11, 12 và 13, đồng thời giải thích rõ ràng các bước thực hiện và các lưu ý quan trọng.
Trang 10 thường chứa các bài tập áp dụng kiến thức cơ bản của mục 3. Các bài tập này thường yêu cầu học sinh thực hiện các phép tính đơn giản, chứng minh các đẳng thức hoặc giải các phương trình, bất phương trình cơ bản. Dưới đây là lời giải chi tiết cho từng bài tập:
Trang 11 thường chứa các bài tập nâng cao hơn, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn. Các bài tập này có thể liên quan đến việc giải các bài toán thực tế, chứng minh các định lý hoặc tìm các giá trị tối đa, tối thiểu. Dưới đây là lời giải chi tiết cho từng bài tập:
Trang 12 tiếp tục cung cấp các bài tập vận dụng và mở rộng kiến thức. Các bài tập này có thể yêu cầu học sinh kết hợp nhiều kiến thức khác nhau để giải quyết một vấn đề. Dưới đây là lời giải chi tiết cho từng bài tập:
Trang 13 thường chứa các bài tập tổng hợp, giúp học sinh củng cố kiến thức và kỹ năng đã học trong mục 3. Các bài tập này có thể yêu cầu học sinh giải quyết các bài toán phức tạp, đòi hỏi sự sáng tạo và tư duy logic. Dưới đây là lời giải chi tiết cho từng bài tập:
Để giải bài tập Toán 11 Chuyên đề học tập - Cánh diều một cách hiệu quả, bạn nên:
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải quyết các bài tập trong mục 3 trang 10, 11, 12, 13 Chuyên đề học tập Toán 11 - Cánh diều. Chúc bạn học tập tốt!