Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều

Bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Hình 41 là hình viên gạch men.

Đề bài

Hình 41 là hình viên gạch men.

a) Xác định tâm đối xứng của viên gạch.

b) Xác định các trục đối xứng của viên gạch.

c) Xác định ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay \(\varphi = 90^\circ .\)

Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều 2

Dựa vào định nghĩa để xác định:

- Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d. Kí hiệu \({Đ_d}\).

- Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.

Lời giải chi tiết

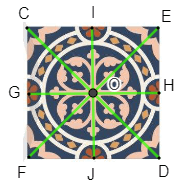
Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều 3

a) Tâm đối xứng của viên gạch là điểm O.

b) Viên gạch có 4 trục đối xứng là các đường thẳng IJ, GH, EF, CD.

c) Viên gạch có dạng hình vuông nên hai đường chéo CD và EF vuông góc với nhau tại tâm đối xứng O và O là trung điểm của mỗi đường chéo nên \(OE{\rm{ }} = {\rm{ }}OC{\rm{ }} = {\rm{ }}OF{\rm{ }} = {\rm{ }}OD\) và \(\widehat {EOC} = \widehat {{\rm{COF}}} = \widehat {FOD} = \widehat {DOE} = 90^\circ \).

Vì phép quay với góc quay \(\varphi = 90^\circ \) có chiều quay ngược chiều kim đồng hồ.

Do đó, ta có phép quay tâm O, góc quay \(\varphi = 90^\circ \) biến các điểm E, C, F, D tương ứng thành các điểm C, F, D, E.

Từ đó suy ra ảnh của viên gạch qua phép quay tâm O (tâm đối xứng của viên gạch) với góc quay \(\varphi = 90^\circ \) chính là viên gạch đó.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục toán 11 trên nền tảng toán math. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều thuộc chương trình học về đạo hàm. Để giải quyết bài toán này, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Phần 1: Đề bài và phân tích yêu cầu

Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều:

(Đề bài cụ thể sẽ được chèn vào đây - ví dụ: Cho hàm số y = f(x) = x^3 - 3x^2 + 2. Tìm đạo hàm f'(x) và xác định các điểm cực trị của hàm số.)

Yêu cầu của bài toán là tìm đạo hàm của hàm số đã cho và xác định các điểm cực trị. Để làm được điều này, chúng ta cần thực hiện các bước sau:

Tính đạo hàm f'(x) của hàm số f(x).
Giải phương trình f'(x) = 0 để tìm các điểm nghiệm.
Xác định dấu của f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
Kết luận về các điểm cực trị của hàm số.

Phần 2: Giải chi tiết bài 7 trang 24

Bước 1: Tính đạo hàm f'(x)

Sử dụng quy tắc tính đạo hàm của tổng và tích, ta có:

f'(x) = d/dx (x^3 - 3x^2 + 2) = 3x^2 - 6x

Bước 2: Giải phương trình f'(x) = 0

Để tìm các điểm nghiệm, ta giải phương trình:

3x^2 - 6x = 0

⇔ 3x(x - 2) = 0

⇔ x = 0 hoặc x = 2

Bước 3: Xác định dấu của f'(x)

Ta xét các khoảng sau:

Khoảng (-∞, 0): Chọn x = -1, f'(-1) = 3(-1)^2 - 6(-1) = 9 > 0. Vậy hàm số đồng biến trên khoảng (-∞, 0).
Khoảng (0, 2): Chọn x = 1, f'(1) = 3(1)^2 - 6(1) = -3 < 0. Vậy hàm số nghịch biến trên khoảng (0, 2).
Khoảng (2, +∞): Chọn x = 3, f'(3) = 3(3)^2 - 6(3) = 9 > 0. Vậy hàm số đồng biến trên khoảng (2, +∞).

Bước 4: Kết luận về các điểm cực trị

Dựa vào dấu của f'(x), ta có thể kết luận:

Tại x = 0, hàm số đổi từ đồng biến sang nghịch biến, nên x = 0 là điểm cực đại. Giá trị cực đại là f(0) = 0^3 - 3(0)^2 + 2 = 2.
Tại x = 2, hàm số đổi từ nghịch biến sang đồng biến, nên x = 2 là điểm cực tiểu. Giá trị cực tiểu là f(2) = 2^3 - 3(2)^2 + 2 = -2.

Phần 3: Tổng kết và lưu ý

Vậy, bài 7 trang 24 Chuyên đề học tập Toán 11 Cánh diều đã được giải quyết hoàn chỉnh. Qua bài giải này, chúng ta đã củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.

Lưu ý: