Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chuyên đề học tập của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 2 của Chuyên đề học tập Toán 11 - Cánh diều tập trung vào các kiến thức quan trọng. Việc giải đúng các bài tập trang 36, 37, 38, 39 là bước đệm quan trọng để hiểu sâu hơn về các khái niệm và ứng dụng trong toán học.
Đọc tên các đỉnh, các cạnh của đồ thị ở Hình 2c.
Có năm thành phố A, B, C, D, E sao cho hai thành phố bất kì trong chúng đều có đúng một đường nối với nhau. Sử dụng đồ thị để mô tả tình huống đó.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
Sử dụng điểm để biểu diễn vị trí thành phố, đoạn thẳng biểu diễn đường đi giữa hai thành phố, ta có mô hình như hình dưới đây.
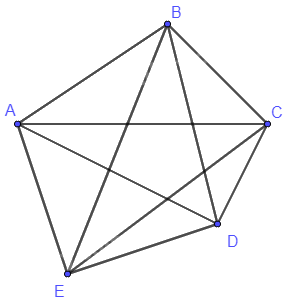
Quan sát đồ thị Hình 8 và cho biết hai đỉnh bất kì của đồ thị có được nối với nhau bằng một đường đi hay không?
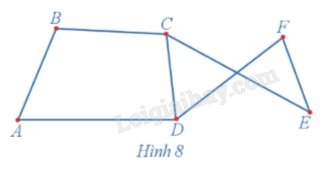
Phương pháp giải:
- Trong một đồ thị, dãy các cạnh kế tiếp nhau AB, BC,…,MN, NP được gọi là đường đi từ đỉnh A đến P, kí hiệu ABC…MNP.
- Quan sát hình 8 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 8 ta thấy hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Quan sát đồ thị Hình 7 và cho biết:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh hay không;
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có đặc điểm gì.
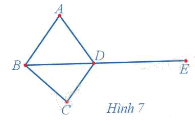
Phương pháp giải:
Quan sát hình 7 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 7 ta thấy:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh của đồ thị.
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có những tính chất sau: không có cạnh nào xuất hiện hai lần, đỉnh cuối của cạnh bất kì là đỉnh đầu của cạnh tiếp theo và không có đỉnh nào được đi qua hai lần. Dãy các cạnh kế tiếp nhau AB, BC, CD, DE được gọi là một đường đi từ đỉnh A đến đỉnh E.
Cho ví dụ về một đồ thị có số lẻ đỉnh bậc chẵn.
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
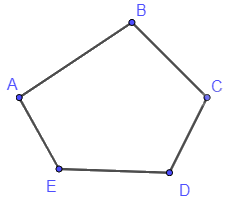
Đồ thị trên có 5 đỉnh A, B, C, D, E với d(A) = d(B) = d(C) = d(D) = d(E) = 2.
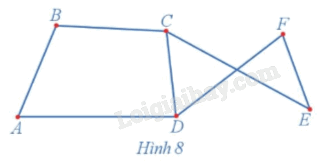
Trong đồ thị ở Hình 8, hãy tìm:
a) Một đường đi từ đỉnh A đến đỉnh F;
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối.
Phương pháp giải:
Trong một đồ thị, dãy các cạnh kế tiếp nhau AB, BC,…,MN, NP được gọi là đường đi từ đỉnh A đến P, kí hiệu ABC…MNP.
Lời giải chi tiết:
a) Một đường đi từ đỉnh A đến đỉnh F là ADE (hoặc có thể chọn ABCDF hoặc ABCEF).
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối là ECDFE (hoặc có thể chọn EFDCE).
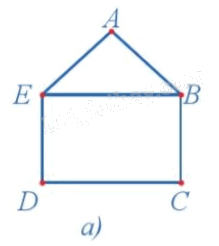
Có bao nhiêu đỉnh bậc lẻ trong đồ thị ở Hình 5a?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
Quan sát Hình 5a ta thấy d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 2 và d(E) = 3 nên B, E là các đỉnh bậc lẻ. Vậy có hai đỉnh bậc lẻ trong đồ thị ở Hình 5a.
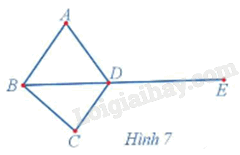
Quan sát đồ thị Hình 7 và cho biết:
a) Tổng các bậc của năm đỉnh trong đồ thị đó;
b) Số cạnh của đồ thị đó;
c) Tổng các bậc của năm đỉnh trong đồ thị gấp bao nhiêu lần số cạnh của đồ thị đó.
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
Quan sát đồ thị Hình 7 ta thấy:
a) d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 4, d(E) = 1.
Do đó, tổng các bậc của năm đỉnh trong đồ thị đó là 2 + 3 + 2 + 4 + 1 = 12.
b) Số cạnh của đồ thị đó là 6.
c) Ta có: 6 . 2 = 12 nên tổng các bậc của năm đỉnh trong đồ thị gấp hai lần số cạnh của đồ thị đó.
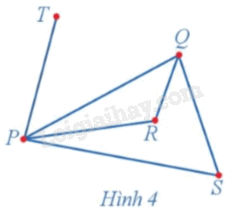
Quan sát đồ thị ở Hình 4 và cho biết:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất bao nhiêu cạnh nối chúng;
b) Có hay không một đỉnh được nối với chính nó bởi một cạnh của đồ thị.
Phương pháp giải:
Quan sát hình 4 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 4 ta thấy:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất một cạnh nối chúng.
b) Không có đỉnh nào được nối với chính nó bởi một cạnh của đồ thị.
Cho hai ví dụ về đồ thị đơn.
Phương pháp giải:
Đồ thị G được gọi là đồ thị đơn nếu với mỗi cặp đỉnh của đồ thị chỉ có không quá một cạnh nối chúng và không có đỉnh nào nối với chính nó bởi một cạnh của đồ thị.
Lời giải chi tiết:
Các đồ thị ở hai hình sau là đồ thị đơn.
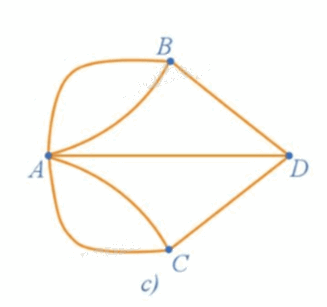
Đọc tên các đỉnh, các cạnh của đồ thị ở Hình 2c.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
Ở đồ thị Hình 2c có:
+ Các đỉnh là: A, B, C, D.
+ Các cạnh là: AB, AC, AD, BA, BD, CA, CD.
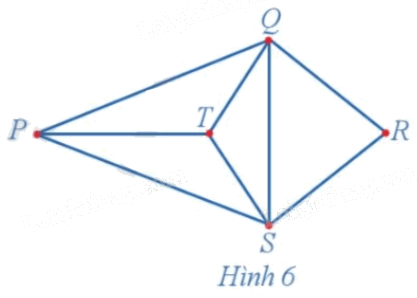
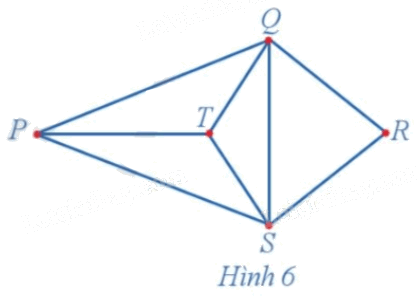
Quan sát đồ thị ở Hình 6 và đếm số cạnh của đồ thị nhận đỉnh P làm đầu mút.
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
Các cạnh của đồ thị nhận đỉnh P làm đầu mút là PQ, PT, PS. Vậy có 3 cạnh của đồ thị nhận đỉnh P làm đầu mút.
Cho ví dụ về một đồ thị liên thông và một đồ thị không liên thông.
Phương pháp giải:
Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Lời giải chi tiết:
+) Ví dụ về đồ thị liên thông:
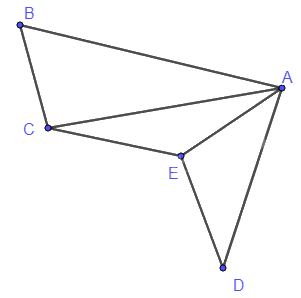
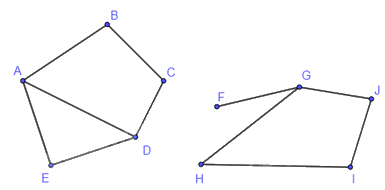
Ở hình trên, hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi. Vậy đồ thị đó là đồ thị liên thông.
+) Ví dụ về đồ thị không liên thông:
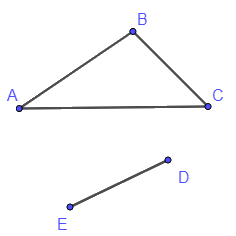
Ở hình trên, mỗi đỉnh thuộc khối bên trên đều không thể nối được với mỗi đỉnh thuộc khối bên dưới bằng một đường đi. Vậy đồ thị đó là đồ thị không liên thông.
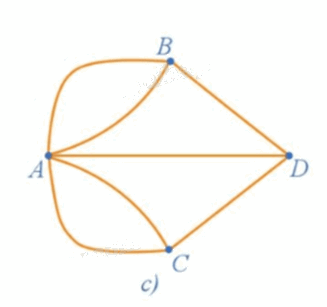
Đọc tên các đỉnh, các cạnh của đồ thị ở Hình 2c.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
Ở đồ thị Hình 2c có:
+ Các đỉnh là: A, B, C, D.
+ Các cạnh là: AB, AC, AD, BA, BD, CA, CD.
Có năm thành phố A, B, C, D, E sao cho hai thành phố bất kì trong chúng đều có đúng một đường nối với nhau. Sử dụng đồ thị để mô tả tình huống đó.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
Sử dụng điểm để biểu diễn vị trí thành phố, đoạn thẳng biểu diễn đường đi giữa hai thành phố, ta có mô hình như hình dưới đây.
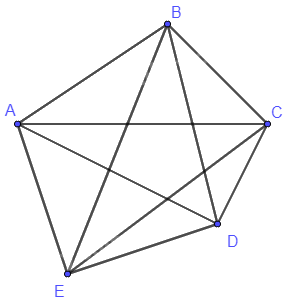
Quan sát đồ thị ở Hình 4 và cho biết:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất bao nhiêu cạnh nối chúng;
b) Có hay không một đỉnh được nối với chính nó bởi một cạnh của đồ thị.
Phương pháp giải:
Quan sát hình 4 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 4 ta thấy:
a) Với mỗi cặp đỉnh của đồ thị, có nhiều nhất một cạnh nối chúng.
b) Không có đỉnh nào được nối với chính nó bởi một cạnh của đồ thị.
Cho hai ví dụ về đồ thị đơn.
Phương pháp giải:
Đồ thị G được gọi là đồ thị đơn nếu với mỗi cặp đỉnh của đồ thị chỉ có không quá một cạnh nối chúng và không có đỉnh nào nối với chính nó bởi một cạnh của đồ thị.
Lời giải chi tiết:
Các đồ thị ở hai hình sau là đồ thị đơn.
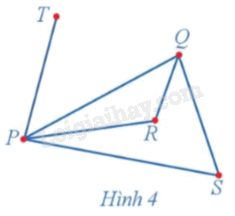
Quan sát đồ thị ở Hình 6 và đếm số cạnh của đồ thị nhận đỉnh P làm đầu mút.
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
Các cạnh của đồ thị nhận đỉnh P làm đầu mút là PQ, PT, PS. Vậy có 3 cạnh của đồ thị nhận đỉnh P làm đầu mút.
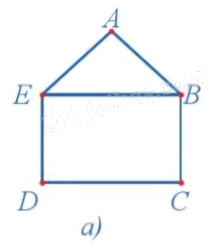
Có bao nhiêu đỉnh bậc lẻ trong đồ thị ở Hình 5a?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
Quan sát Hình 5a ta thấy d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 2 và d(E) = 3 nên B, E là các đỉnh bậc lẻ. Vậy có hai đỉnh bậc lẻ trong đồ thị ở Hình 5a.
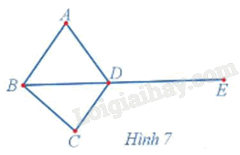
Quan sát đồ thị Hình 7 và cho biết:
a) Tổng các bậc của năm đỉnh trong đồ thị đó;
b) Số cạnh của đồ thị đó;
c) Tổng các bậc của năm đỉnh trong đồ thị gấp bao nhiêu lần số cạnh của đồ thị đó.
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
Quan sát đồ thị Hình 7 ta thấy:
a) d(A) = 2, d(B) = 3, d(C) = 2, d(D) = 4, d(E) = 1.
Do đó, tổng các bậc của năm đỉnh trong đồ thị đó là 2 + 3 + 2 + 4 + 1 = 12.
b) Số cạnh của đồ thị đó là 6.
c) Ta có: 6 . 2 = 12 nên tổng các bậc của năm đỉnh trong đồ thị gấp hai lần số cạnh của đồ thị đó.
Cho ví dụ về một đồ thị có số lẻ đỉnh bậc chẵn.
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Lời giải chi tiết:
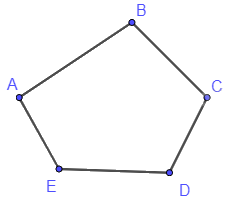
Đồ thị trên có 5 đỉnh A, B, C, D, E với d(A) = d(B) = d(C) = d(D) = d(E) = 2.
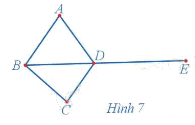
Quan sát đồ thị Hình 7 và cho biết:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh hay không;
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có đặc điểm gì.
Phương pháp giải:
Quan sát hình 7 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 7 ta thấy:
a) Hai đỉnh A, B có được nối với nhau bằng một cạnh của đồ thị.
b) Dãy các cạnh kế tiếp nhau AB, BC, CD, DE có những tính chất sau: không có cạnh nào xuất hiện hai lần, đỉnh cuối của cạnh bất kì là đỉnh đầu của cạnh tiếp theo và không có đỉnh nào được đi qua hai lần. Dãy các cạnh kế tiếp nhau AB, BC, CD, DE được gọi là một đường đi từ đỉnh A đến đỉnh E.
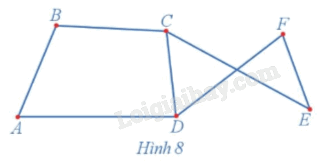
Trong đồ thị ở Hình 8, hãy tìm:
a) Một đường đi từ đỉnh A đến đỉnh F;
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối.
Phương pháp giải:
Trong một đồ thị, dãy các cạnh kế tiếp nhau AB, BC,…,MN, NP được gọi là đường đi từ đỉnh A đến P, kí hiệu ABC…MNP.
Lời giải chi tiết:
a) Một đường đi từ đỉnh A đến đỉnh F là ADE (hoặc có thể chọn ABCDF hoặc ABCEF).
b) Một chu trình có đỉnh E là đỉnh đầu và đỉnh cuối là ECDFE (hoặc có thể chọn EFDCE).
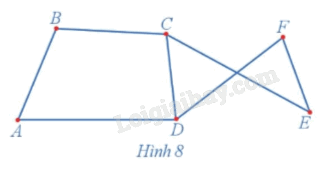
Quan sát đồ thị Hình 8 và cho biết hai đỉnh bất kì của đồ thị có được nối với nhau bằng một đường đi hay không?
Phương pháp giải:
- Trong một đồ thị, dãy các cạnh kế tiếp nhau AB, BC,…,MN, NP được gọi là đường đi từ đỉnh A đến P, kí hiệu ABC…MNP.
- Quan sát hình 8 để trả lời
Lời giải chi tiết:
Quan sát đồ thị Hình 8 ta thấy hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Cho ví dụ về một đồ thị liên thông và một đồ thị không liên thông.
Phương pháp giải:
Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Lời giải chi tiết:
+) Ví dụ về đồ thị liên thông:
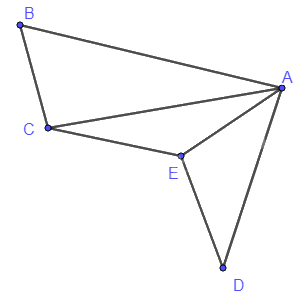
Ở hình trên, hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi. Vậy đồ thị đó là đồ thị liên thông.
+) Ví dụ về đồ thị không liên thông:
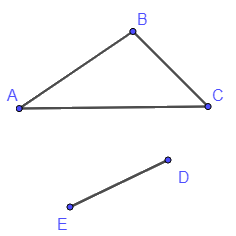
Ở hình trên, mỗi đỉnh thuộc khối bên trên đều không thể nối được với mỗi đỉnh thuộc khối bên dưới bằng một đường đi. Vậy đồ thị đó là đồ thị không liên thông.
Mục 2 trong Chuyên đề học tập Toán 11 - Cánh diều thường xoay quanh một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trang 36, 37, 38, 39 không chỉ giúp củng cố kiến thức mà còn rèn luyện tư duy logic và khả năng áp dụng công thức vào thực tế.
Để hiểu rõ hơn về Mục 2, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, đây có thể là một chương về hàm số, phương trình, bất phương trình, hoặc các khái niệm hình học không gian. Việc nắm bắt được nội dung chính sẽ giúp học sinh tập trung vào những kiến thức quan trọng và tránh lan man.
Để giải các bài tập trong Mục 2 một cách hiệu quả, học sinh cần áp dụng các phương pháp sau:
Bài 1: (Đề bài cụ thể của bài 1)...
Lời giải: (Giải chi tiết bài 1, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng)...
Bài 2: (Đề bài cụ thể của bài 2)...
Lời giải: (Giải chi tiết bài 2, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng)...
Bài 3: (Đề bài cụ thể của bài 3)...
Lời giải: (Giải chi tiết bài 3, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng)...
Bài 4: (Đề bài cụ thể của bài 4)...
Lời giải: (Giải chi tiết bài 4, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng)...
Bài 5: (Đề bài cụ thể của bài 5)...
Lời giải: (Giải chi tiết bài 5, bao gồm các bước giải, công thức sử dụng, và kết quả cuối cùng)...
Trong quá trình giải bài tập, học sinh cần chú ý đến các dấu hiệu đặc biệt, các điều kiện ràng buộc, và các trường hợp ngoại lệ. Việc bỏ qua những chi tiết nhỏ có thể dẫn đến kết quả sai lệch.
Kiến thức trong Mục 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học và khoa học tự nhiên. Ví dụ, kiến thức về hàm số được sử dụng để mô tả các hiện tượng vật lý, kiến thức về phương trình được sử dụng để giải các bài toán kỹ thuật, và kiến thức về bất phương trình được sử dụng để tối ưu hóa các quá trình sản xuất.
Việc giải các bài tập trang 36, 37, 38, 39 trong Mục 2 của Chuyên đề học tập Toán 11 - Cánh diều là một bước quan trọng trong quá trình học tập toán học. Bằng cách áp dụng các phương pháp giải bài tập hiệu quả và nắm vững kiến thức lý thuyết, học sinh có thể tự tin giải quyết các bài toán khó và đạt kết quả cao trong các kỳ thi.